In this assignment you are going to implement a few algorithms which, when put together, form a machine learning model to detect fraudulent credit card transactions. The model you will implement is a (very) simplified version of one that could be employed in the real world. In this process, you will employ a number of algorithms covered throughout this course.

Note: before reading the assignment you might want to watch the accompanying video that gives a brief description of the assignment and its context. The video is available on the Ed post where the assignment was released.

The base problem

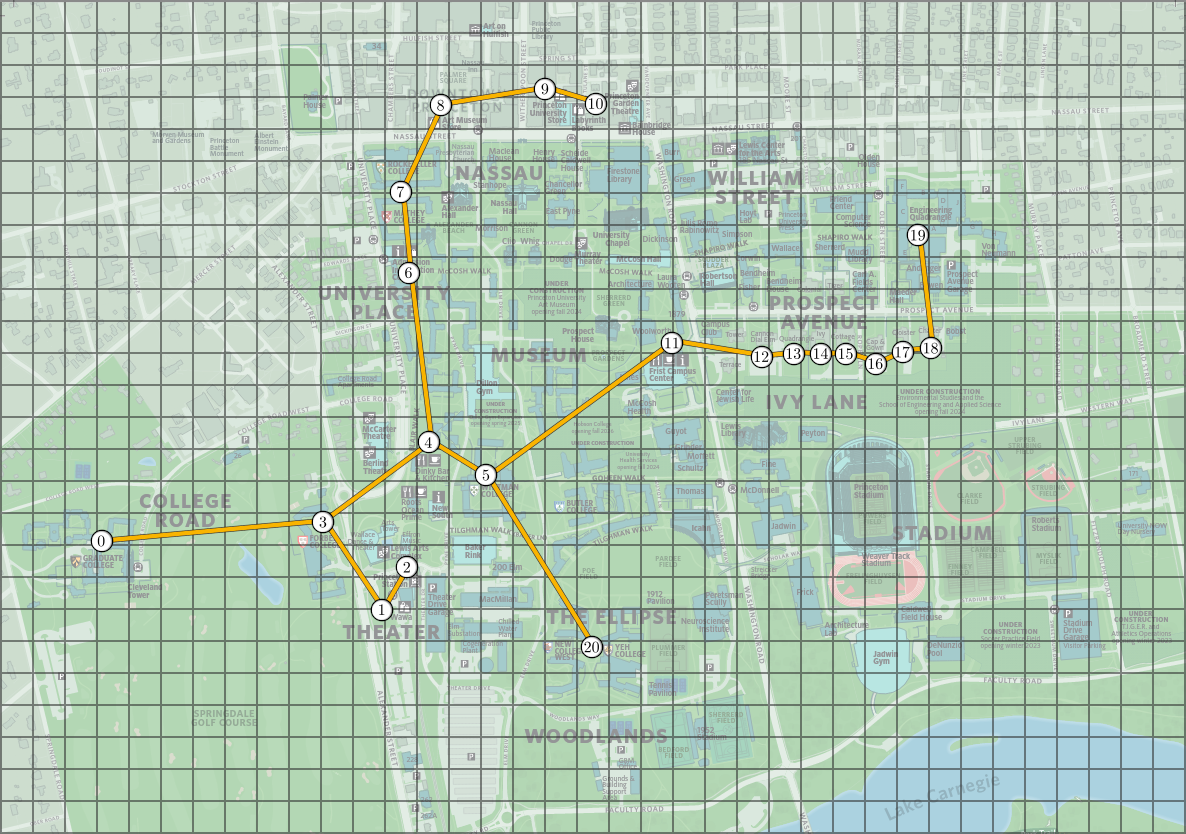
Consider a set of \(m\) points in 2D space, each representing coordinates of retail establishments, such as shops and restaurants, on a map. These points are represented using the immutable data type Point2D (part of algs4.jar). Below is an example of locations in a map of Princeton.

\(m = 21\) locations in Princeton (click to enlarge)
Princeton Locations

Additionally, you are given a data set with \(n\) labeled transaction summaries. In your implementation you can assume \(n\) is always at least 1. A transaction summary is an array of \(m\) non-negative integers, one per location, representing the amount of money spent at each location by a particular person. A label is either clean or fraud, indicating whether a fraudulent transaction was detected in the corresponding transaction summary. Here is an example of one. Each number corresponds to a location in the map (e.g. the first number represents the amount of money spent at "Graduate College," the leftmost point).

a transaction summary
  5     6     7     0     6     7     5     6     7     0     6     7     0     6     7     0     6     7     0     6     7     clean  

You will create a simple machine learning model that learns from a data set. That is, you will be given a collection of labeled transaction summaries and write an algorithm that labels new transaction summaries as either clean or fraud. These labels are represented by integers: 0 for clean and 1 for fraud.

Dimensionality reduction

Before feeding the data into the machine learning model, you will first reduce the dimension of the input (i.e. the transaction summaries) using a clustering algorithm. This algorithm receives \(m\) locations, as objects of type Point2D, as well as a number \(k\) (between 1 and \(m\)) of clusters. The goal is to output a partition of the points into \(k\) clusters (i.e., groups), such that the points in the same cluster are similar; in our case, two points are similar if the Euclidean distance between them is small.

This step is applied not only to make the model more efficient, but it also improves its accuracy by mitigating an overfit of the model to the input data.

Here is what the clustering algorithm should do:

You don't have to implement all these steps from scratch; there are several helpful classes in algs4.jar that you can use (see the implementation requirements below).

The following images represent the minimum spanning tree and the clusters obtained from the Princeton locations above, with \(k = 5\) clusters. In the image to the right, clusters are indicated by colors and dashed lines represent the edges of the minimum spanning tree that are excluded from the cluster graph.

Minimum spanning tree and the \(k = 5\) clusters of the \(m = 21\) locations in the Princeton graph (click to enlarge)
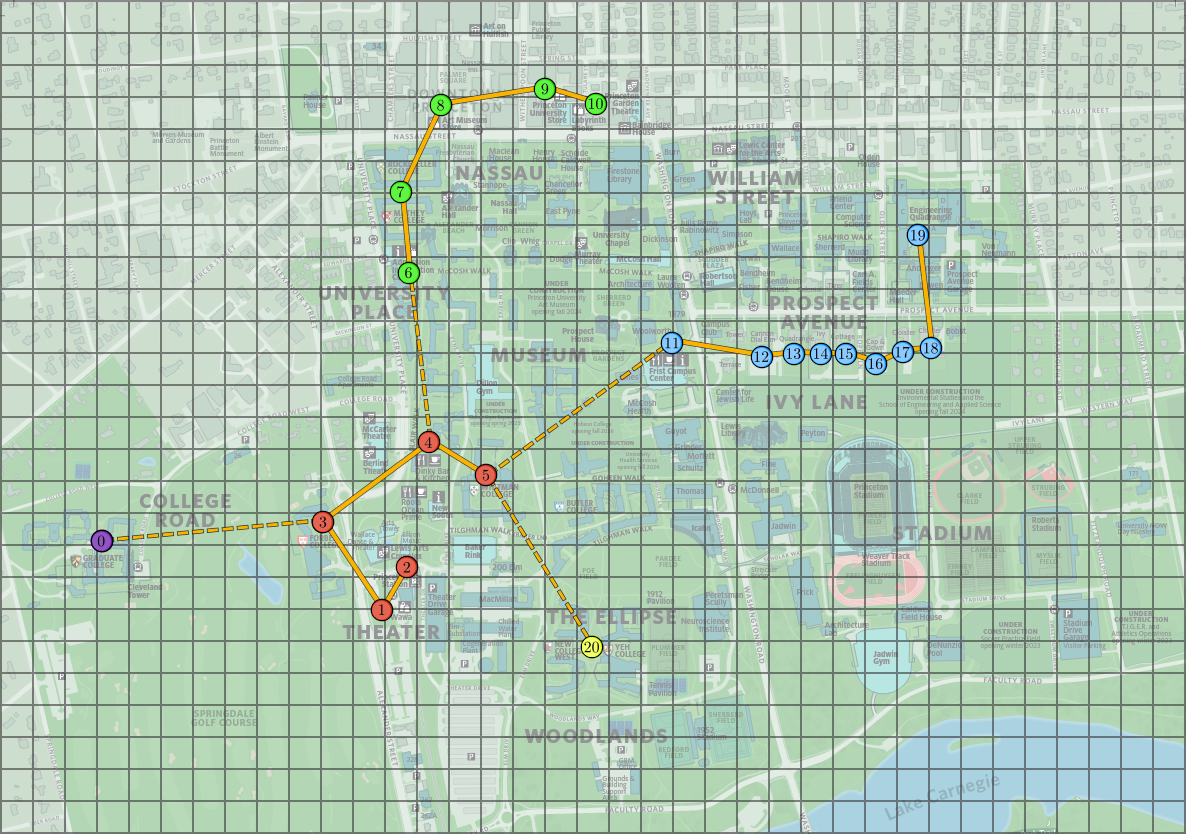
Minium Spanning Tree of Princeton Locations Clusters of Princeton Locations

We can now reduce the dimension of each transaction summary by summing all of the entries corresponding to the same cluster, which yields a new array with \(k\) (reduced from \(m\)) elements. This is illustrated below, where each color labels a cluster in the image above.

dimensionality reduction in a transaction summary
  5     6     7     0     6     7     5     6     7     0     6     7     0     6     7     0     6     7     0     6     7     Original  
  5     26     24     39     7     Reduced  

To help you test your code, we provide the file princeton_locations.txt formatted as follows: the first line contains the number \(m\) of locations, followed by \(m\) lines with the \((x, y)\) coordinates of each location. The order of the points matches the above images (e.g., the first point represents "Graduate College"). We also include princeton_locations_mst.txt, which contains the edges of the Euclidean graph's the minimum spanning tree.

Clustering Algorithm. Implement an immutable data type Clustering with the following API: 

public class Clustering {

    // run the clustering algorithm and create the clusters  
    public Clustering(Point2D[] locations, int k)

    // return the cluster of the ith location 
    public int clusterOf(int i)

    // use the clusters to reduce the dimensions of an input 
    public int[] reduceDimensions(int[] input)

    // unit testing (required)
    public static void main(String[] args)
}

Note that clusterOf() must return an integer between \(0\) and \(k-1\) satisfying the following condition: clusterOf(i) and clusterOf(j) are equal if and only if the \(i\)th and \(j\)th points belong to the same cluster.

Implementation requirements.  You should use KruskalMST and CC to compute a minimum spanning tree and connected components of the cluster graph.

Corner cases.  Throw an IllegalArgumentException if:

Unit testing.  In your main() method you will implement a test that generates a set of points whose clustering is known in advance. More precisely, you will generate a set of locations that form tight "point clouds" centered at random points that are far away from each other. Here is a thorough description of what you need to do:

You should test your implementation with values of \(c\) and \(p\) around \(50\) and it should take up to a few seconds to run.

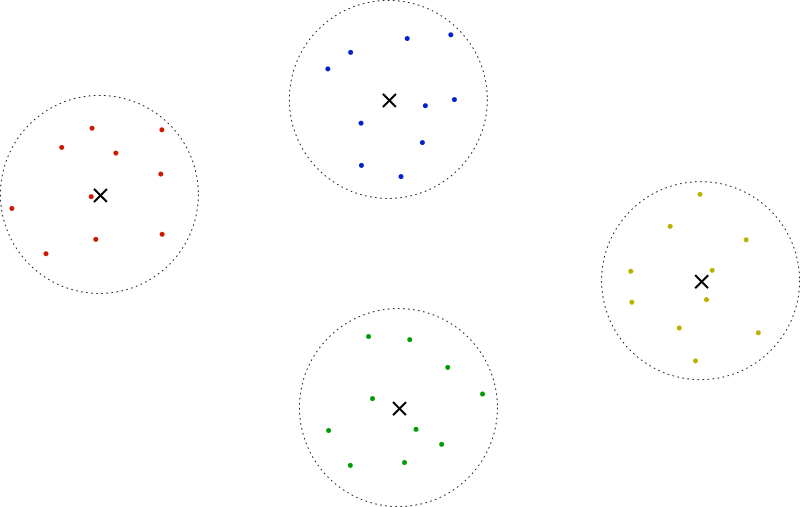
The key reason this works is that points around the same center are closer to each other than to any other point, so they necessarily end up in the same cluster. The image below shows an example with \(c = 4\) centers, represented by crosses, and \(p = 10\) points per center. Each circumference around a center has radius 1 and represents the space of possible locations of the points around that center. Note that the point cloud centers are only for visualization purposes, they don't correspond to locations.

Performance requirements.  Your implementation must achieve the following performance requirements:

Weak learners

A weak learner is a machine learning model that performs marginally better than a random decision. In the context of this assignment, this means predicting the right label more than \(50\%\) of the time. You will implement a model known as a decision stump, a really popular choice for weak learners.

Your decision stump takes as input a sequence of \(n\) dimension-reduced transaction summaries, each of which is an array of \(k\) integers. In other words, the input is a 2-dimensional \(n \times k\) array of integers input[][], where input[i][j] is the amount of money the reduced transaction summary i spent at cluster j. Each input is labeled with an integer, either 0 or 1 (corresponding to clean or fraud, respectively), given in an integer array labels[] of length \(n\). Each input is also associated to a non-negative weight, given by the double[] length-\(n\) array weights[] (which will be used in the last part of this assignment).

From the input data and labels, the decision stump "learns" a predictor: a function that takes a single sample (i.e. a new transaction summary given as an array of \(k\) integers) as input and outputs a binary prediction, 0 or 1 (i.e. clean or fraud). This predictor is a very simple function which we describe in the following paragraphs.

Note: the following description might seem a bit overwhelming at first. Try to read all of it, then study the examples in the images; the visual representations are really helpful to understand the description.

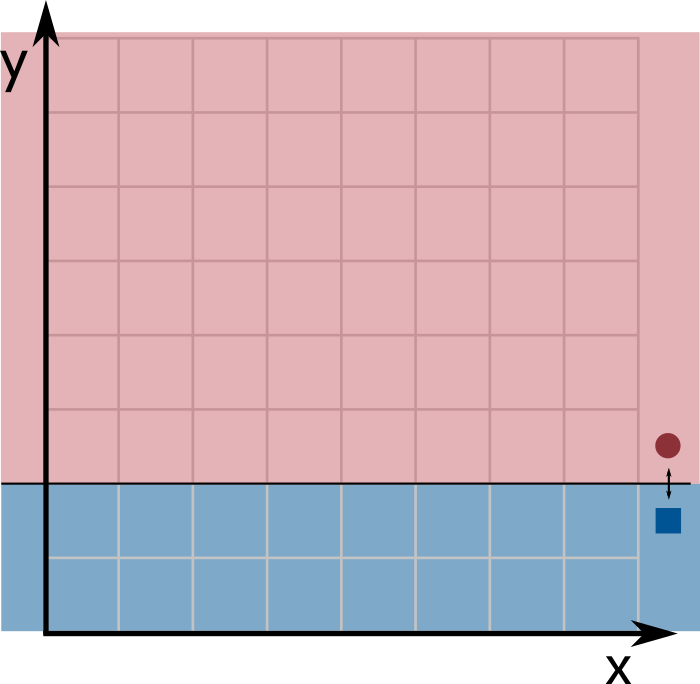
Since each input is an array of length \(k\), we can think about them as a points in \(k\)-dimensional space (i.e. the \(x\) coordinate corresponds to the 0 index of the input array, the \(y\) coordinate corresponds to the 1 index of the input array, and so on). A decision stump classifies a point based on a single coordinate of the point. For example, \(x \leq 4\) is the decision stump that labels all points with \(x\) coordinate value less than or equal to \(4\) as 0 and all other points as 1. This definition has a nice geometric interpretation: a decision stump corresponds to a (hyper)plane perpendicular to one of the axes. Given one such (hyper)plane, a decision stump labels all points to one side of that (hyper)plane as 0 and points on the other side as 1. The images below show three examples of decision stumps. The first one has \(k=2\) and corresponds to \(y \leq 2\). The second one has \(k=2\) and corresponds to \(x \leq 5\). The third one has \(k=3\) and corresponds to \(y \geq 4\).

Three decision stumps (click to enlarge)

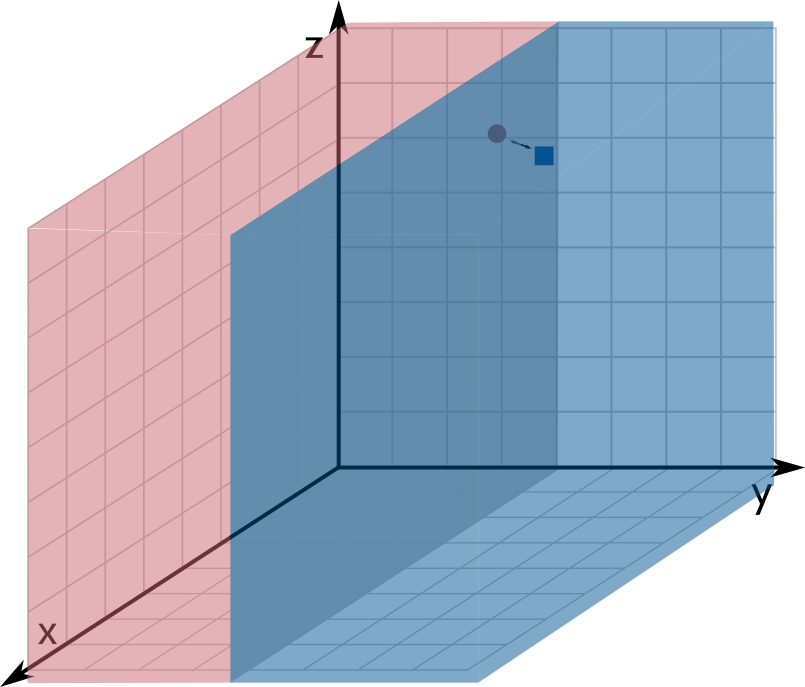
Decision Stump 1                   Decision Stump 2                   Decision Stump 3

Based on the above, we will use three integers to describe a decision stump: a dimension predictor \(d_p\), a value predictor \(v_p\) and a sign predictor \(s_p\). The dimension predictor is an integer between \(0\) and \(k - 1\), which represents the dimension/coordinate of the input space that is partitioned (into the region classified as 0 and the region classified as 1). The value predictor is an integer that determines where the input space is partitioned (i.e. where the hyperplane crosses its perpendicular axis). The sign predictor is either \(0\) or \(1\), and determines the direction of the labels, i.e. which side of the plane gets classified as 0 and which gets classified as 1.

Given a \(k\)-dimensional input point \(\textsf{sample}\), a decision stump with parameters \(d_p\), \(v_p\) and \(s_p\) labels it according to the following rule:

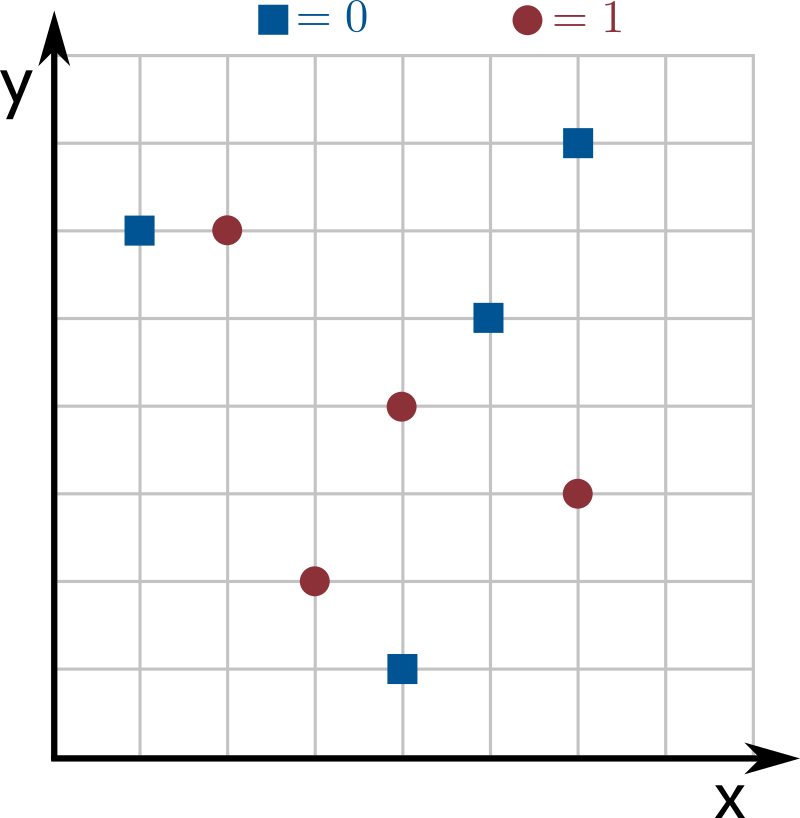
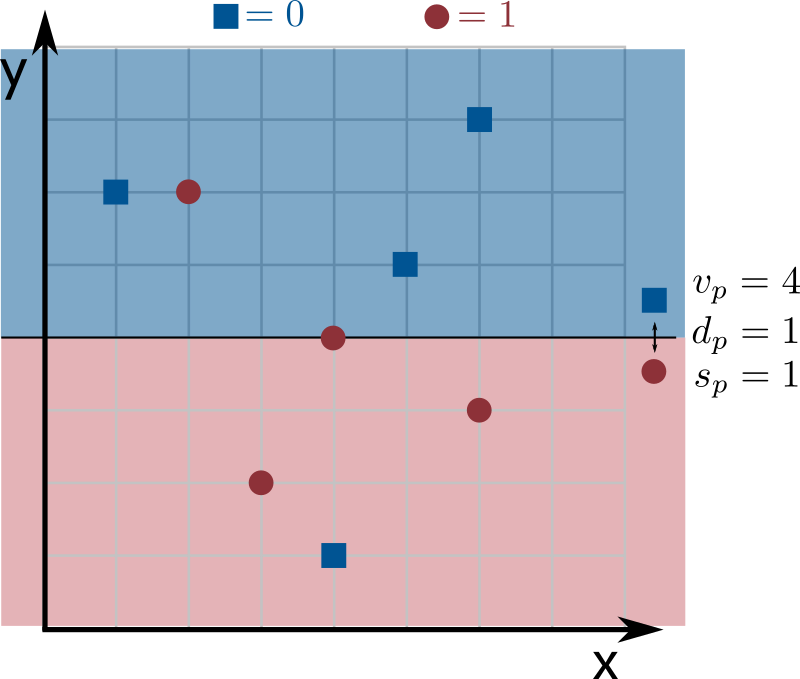
See the images below for an example with \(n = 8\) inputs of dimension \(k = 2\), where dimensions 0 and 1 correspond to the the x and y axes, respectively. Blue squares correspond to the label 0 and red circles to the label 1. The line in the image is the hyperplane that splits dimension \(d_p = 1\) at coordinate \(v_p = 4\) into two regions: since \(s_p = 1\), points above the line (of \(y\) coordinate larger than \(4\)) are labeled as 0, and points at or below the line (of \(y\) coordinate smaller than or equal to \(4\)) are labeled as 1.

Points on a grid and weak learner predictor (\(n = 8\), \(k = 2\)) (click to enlarge)
Grid of points                   Predictor on grid

Your goal is to find the decision stump that best represents the input data (we call this step training the model). That is, your task is to find the values of \(d_p\), \(v_p\) and \(s_p\) that maximize the weight of correctly classified inputs, (i.e., maximizes the sum of the weights of the inputs whose predicted label matches the corresponding value in labels[]).

If all points have weight \(1\) in the image above, the weight of correctly classified inputs by the given decision stump is \(6\) (all points are correctly classified except for one blue square and one red circle). Since no other decision stump mislabels fewer than 2 points, it is optimal (i.e., is the stump that best represents the training data).

Weak Learner. Implement an immutable data type class WeakLearner with the following API: 

public class WeakLearner {

    // train the weak learner  
    public WeakLearner(int[][] input, double[] weights, int[] labels)

    // return the prediction of the learner for a new sample  
    public int predict(int[] sample)

    // return the dimension the learner uses to separate the data  
    public int dimensionPredictor()

    // return the value the learner uses to separate the data 
    public int valuePredictor()

    // return the sign the learner uses to separate the data 
    public int signPredictor()

    // unit testing
    public static void main(String[] args)
}

Corner cases.  Throw an IllegalArgumentException if:

Unit testing.  You don't need to create unit tests. Use the visualizer and the examples in the Checklist to test your implementation.

Performance requirements.  Your implementation must achieve the following performance requirements:

Note: it is very easy to miss some corner cases in your implementation of this class. To debug your code using good test cases, read the Checklist section on testing.

Boosting algorithm

As the name suggests, the weak learner is not a very interesting model. You will now implement a better one using a technique called boosting: taking weak learners and improving (boosting) their quality. In this assignment you will implement a simplified version of AdaBoost (short for Adaptive Boosting), which is an application of the multiplicative weights algorithm.

The input consists of a sequence of \(n\) labeled (non-reduced) transaction summaries is given as an \(n \times m\) integer array input[][]); the \(m\) map locations (a Point2D[] array of length \(m\)); as well as an integer \(k\) (the number of clusters to cluster the locations into). You should start by creating a Clustering object so you can map transaction summaries into arrays of length \(k\), using the dimensionality reduction method. From now on, we will use "input" to refer to the reduced transaction summaries, i.e. the \(n \times k\) array resulting from applied the dimensionality reduction method to the original transaction summaries.

AdaBoost is a version of multiplicative weights where the input points are the experts. The algorithm assigns a weight to each input point, represented as a double[] array of length \(n\). This array is normalized, so that the sum of its elements is always \(1\). Initially, the weights should all be set to the same value: \(1 / n\).

The boosting algorithm works in steps or iterations. Each iteration proceeds as follows:

We double the weight of mislabeled inputs to force the algorithm to try harder to predict them correctly in future iterations.

Given a sample (i.e. an \(m\)-dimensional integer array corresponding to a new transaction summary) to make a prediction on, the boosted model should output the majority vote over the predictions given by the weak learner created in each iteration. This means you should use each weak learner created in each iteration to label the sample point, and then output the label that was predicted most often. In case of a tie, output 0. Note that a sample needs to be reduced before you can apply the model.

Boosting Algorithm. Implement a mutable data type BoostingAlgorithm with the following API: 

public class BoostingAlgorithm {

    // create the clusters and initialize your data structures
    public BoostingAlgorithm(int[][] input, int[] labels, Point2D[] locations, int k)

    // return the current weight of the ith point
    public double weightOf(int i)

    // apply one step of the boosting algorithm 
    public void iterate()

    // return the prediction of the learner for a new sample 
    public int predict(int[] sample)

    // unit testing
    public static void main(String[] args)
}

Corner cases.  Throw an IllegalArgumentException if:

Unit testing.  You don't need to create unit tests. We provide you with some code to help you test your BoostingAlgorithm.java implementation. See the section on "Using the learners" below.

Performance requirements.  Your implementation must achieve the following performance requirements:

Using the learners

A typical strategy for testing machine learning models is to partition labeled data into two data sets: a training and a test data set. The model is trained using the training data, and then tested on the test data set. We assess the quality of the model using a very simple metric called accuracy: the fraction of correct predictions. This metric can be used on the training and/or test datasets.

We provide several files that have been pre-partitioned into training and test data sets, named accordingly. Below is a sample client to test the BoostingAlgorithm model. It takes two filenames (training and test data set files), an integer \(k\) (the number of clusters for dimensionality reduction), and an integer \(T\) (the number of iterations of the boosting algorithm) as command-line arguments. It trains the model on the training data set and calculates the accuracy in the training and test data sets. It uses an additional data type DataSet that is provided in the project folder. 

public static void main(String[] args) {
    // read in the terms from a file
    DataSet training = new DataSet(args[0]);
    DataSet testing = new DataSet(args[1]);
    int k = Integer.parseInt(args[2]);
    int T = Integer.parseInt(args[3]);

    int[][] trainingInput = training.getInput();
    int[][] testingInput = testing.getInput();
    int[] trainingLabels = training.getLabels();
    int[] testingLabels = testing.getLabels();
    Point2D[] trainingLocations = training.getLocations();

    // train the model
    BoostingAlgorithm model = new BoostingAlgorithm(trainingInput, trainingLabels,
            trainingLocations, k);
    for (int t = 0; t < T; t++)
        model.iterate();

    // calculate the training data set accuracy
    double training_accuracy = 0;
    for (int i = 0; i < training.getN(); i++)
        if (model.predict(trainingInput[i]) == trainingLabels[i])
            training_accuracy += 1;
    training_accuracy /= training.getN();

    // calculate the test data set accuracy
    double test_accuracy = 0;
    for (int i = 0; i < testing.getN(); i++)
        if (model.predict(testingInput[i]) == testingLabels[i])
            test_accuracy += 1;
    test_accuracy /= testing.getN();

    StdOut.println("Training accuracy of model: " + training_accuracy);
    StdOut.println("Test accuracy of model: " + test_accuracy);
}

To help you test your code, we provide two data sets, one called princeton_training.txt and one called princeton_test.txt. Both use the locations from the map described in the beginning of the assignment, with inputs and labels were generated by a simulation. Here is one example run of the above client on the reference implementation of BoostingAlgorithm: 

~/Desktop/fraud> java-algs4 BoostingAlgorithm princeton_training.txt princeton_test.txt 5 80
Training accuracy of model: 0.9625
Test accuracy of model:     0.7375

Note: Your code might have slightly different accuracy values depending on how your weak learner implementation tie-breaks between decision stumps with the same accuracy. The training accuracy should be around 0.95 and the test accuracy should be around 0.7.

Use this testing framework to run experiments and document them in the readme.txt (the file contains more details on what you should do).

Information about the assignment

Submission.  Submit only Clustering.java, WeakLearner.java and BoostingAlgorithm.java. We will supply algs4.jar. You may not call library functions except those in those in java.lang, java.util, and algs4.jar. Finally, submit readme.txt and acknowledgments.txt files and answer the questions.

Grading.

file points
Clustering.java 8
WeakLearner.java 20
BoostingAlgorithm.java 8
readme.txt 4
40

Reminder: You can lose up to 4 points for breaking style principles and up to 3 points for not implementing the Clustering test.

This assignment was developed by Pedro Paredes.