Frequently Asked Questions (Clustering)

What methods from Points2D can I use? You can use any methods from the Point2D API. Most of the available methods are not necessary, but you may find distanceTo() and/or distanceSquaredTo() useful to compute Euclidean distances.

Do I have to implement both a minimum spanning tree and connected components algorithm from scratch? No! You can use two data types from algs4.jar, namely, KruskalMST and CC, to solve the respective problems.

What exactly is a cluster and why am I computing one? Roughly speaking, a cluster is a group of points that are more alike among themselves than they are to points in other clusters. This is a rather broad definition, and there are many reasonable ways of clustering points (which need not represent locations). We chose to use one based on minimum spanning trees because it works reasonably well with Euclidean graphs, and is based on an algorithm you learned in this course.

You are computing clusters in order to reduce the dimension \(m\) of the input, by contracting all dimensions that are in the same cluster. This improves the efficiency of the classifier that you implement next, since the length of its input arrays becomes \(k\), which is smaller than \(m\). Additionally, if you think about what the underlying machine learning model is doing, grouping together close locations is actually aggregating data in a useful way, so reducing dimensions this way can improve the accuracy of the model too.

What should clusterOf(i) return? There are multiple correct implementations of this method; the only requirement is that the return values be consistent (i.e., that clusterOf(i) == clusterOf(j) if and only if \(i\) and \(j\) belong to the same cluster). For example, clusterOf(0) can return any value between \(0\) and \(k-1\).

How do I generate a random point of distance of at most 1 to another point? You can use a strategy similar to the one you used to generate centers. Suppose you want to generate a point near another point center. Start by generating a random point in the rectangle [(center.x - 1, center.y - 1), (center.x + 1, center.y + 1)]. Check if the distance of this point to center is small enough, if not generate a new random point and repeat until you find a point at the appropriate distance.

Frequently Asked Questions (WeakLearner)

What is the best way to test my implementation? See next section.

When training a weak learner, how should I tie break over two weak learners with the same weight of correctly predicted points? The assignment doesn't specify, so it doesn't matter.

If you are curious about our tie breaking rule, here is what the reference solution does: in case of a tie, always pick the smallest possible dimension predictor, if a tie still persists pick the smallest possible value predictor, and if a tie still yet persists, pick the smallest sign predictor.

I am not sure how to implement the constructor? This is probably the trickiest part of the assignment, so you might have to spend some time thinking about how to do this efficiently. Start by trying to get the less efficient \(O(kn^2)\) solution to work. To do it, notice that you can compute the weight of correct predictions for all possible weak learners. How? Try all possible values of \(d_p\) (there are \(k\) of them), all possible values of \(s_p\) (there are only 2 of them), and all values of \(v_p\), and compute the weight of correct predictions for each one of these weak learners (by looping through all \(n\) input points and computing the weak learner's prediction). But can't \(v_p\) be any possible non-negative integer? Yes, but notice that we only care about values that are coordinates in our input (there are \(n\) of them). A weak learner with a value of \(v_p\) between two coordinates of our input does exactly the same predictions on our input, so its weight of correct predictions is the same. To visualize this, look at the example from the assignment statement:

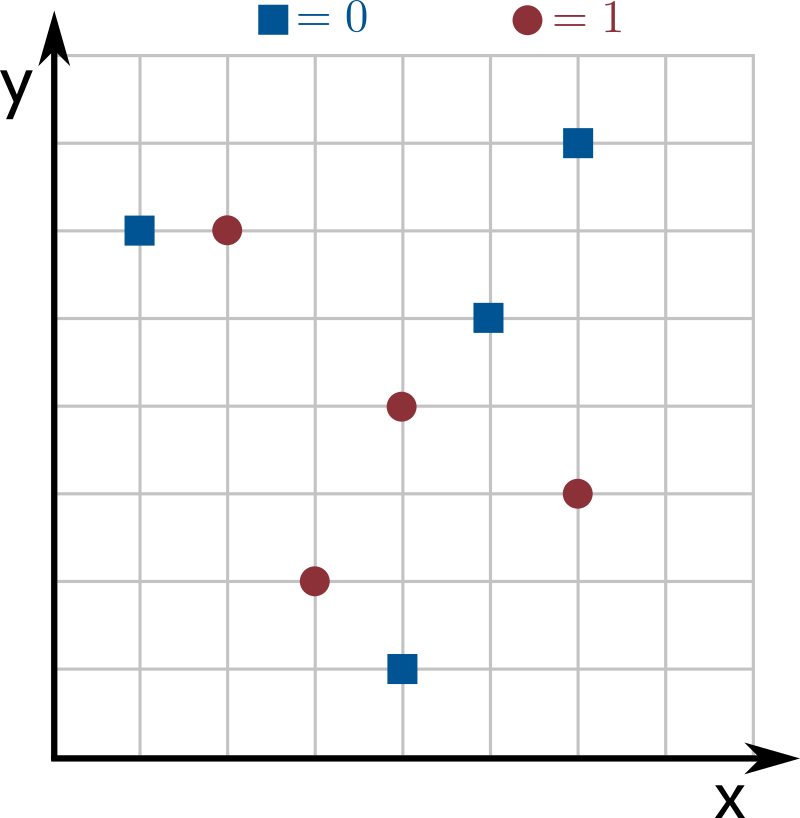
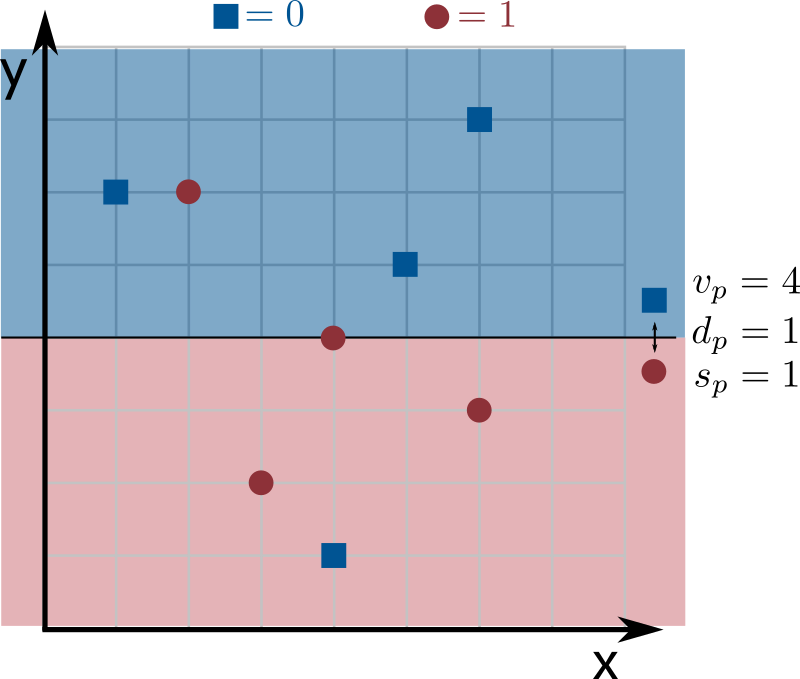
Grid of points                   Predictor on grid

Note that moving the prediction line up by anything less than \(1\) (so setting \(v_p\) to anything at least \(4\) and less than \(5\)) does the exact same predictions on the input.

Once you get this solution to work, think about how to avoid having to repeatedly go through all the points for every possible weak learner, by finding a more clever way to compute the weight of correct predictions without having to go through all points repeatedly. Hint: if you sorted your points by a certain coordinate, could you find the best decision stump for that coordinate efficiently? In other words, suppose you sorted all the points by the \(0\) coordinate, can you find the best decision stump with \(d_p = 0\) in \(\Theta(n)\) time?

Frequently Asked Questions (Testing the WeakLearner)

We created a few small test cases that are good to find corner case bugs in your WeakLearner code, which are stored in the stump_i.txt files. For each one of them, the stump_i.ans.txt contains the parameters of the best decision stump for that particular data set (i.e. what your code should find).

All the examples are based on the point sets of the following images:


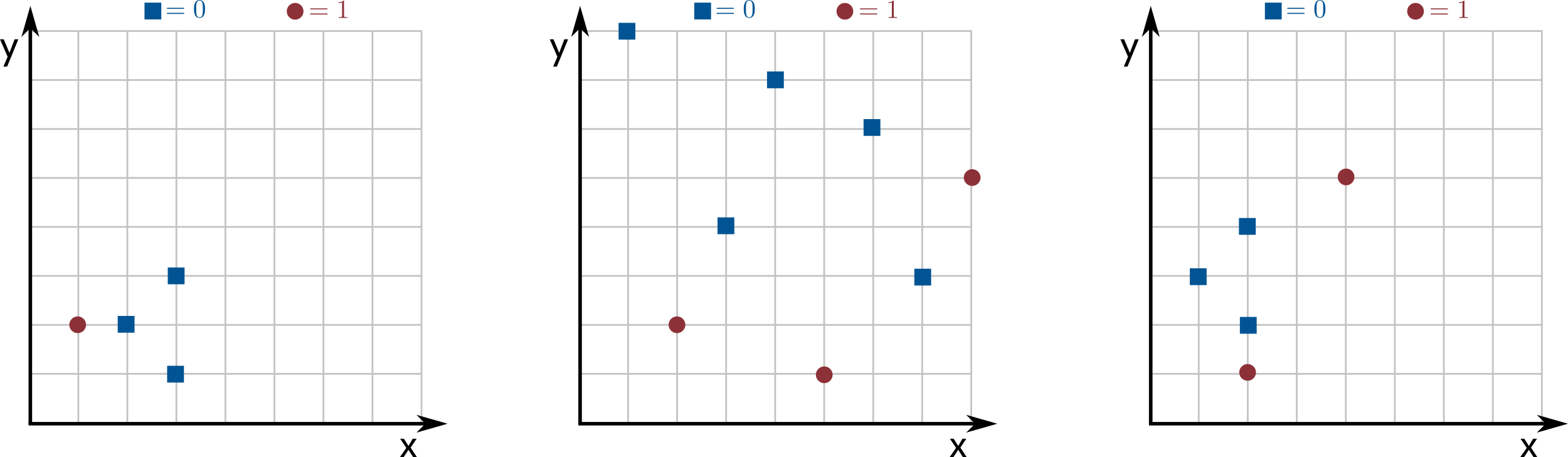
Examples

The first example is helpful to test the basic logic of your implementation. The second two examples help you make sure you are correctly considering the weights in your implementation. The last two examples are helpful to debug one of the most common bugs in the efficient solution, which is forgetting that multiple points can have the same coordinate.

To check these test cases, use the WeakLearnerVisualizer.java client that we provide in the project folder. Once you compile it (note: it needs a fully implemented WeakLearner), you can run it using the following command: 

~/Desktop/fraud> java-algs4 WeakLearnerVisualizer stump_1.txt

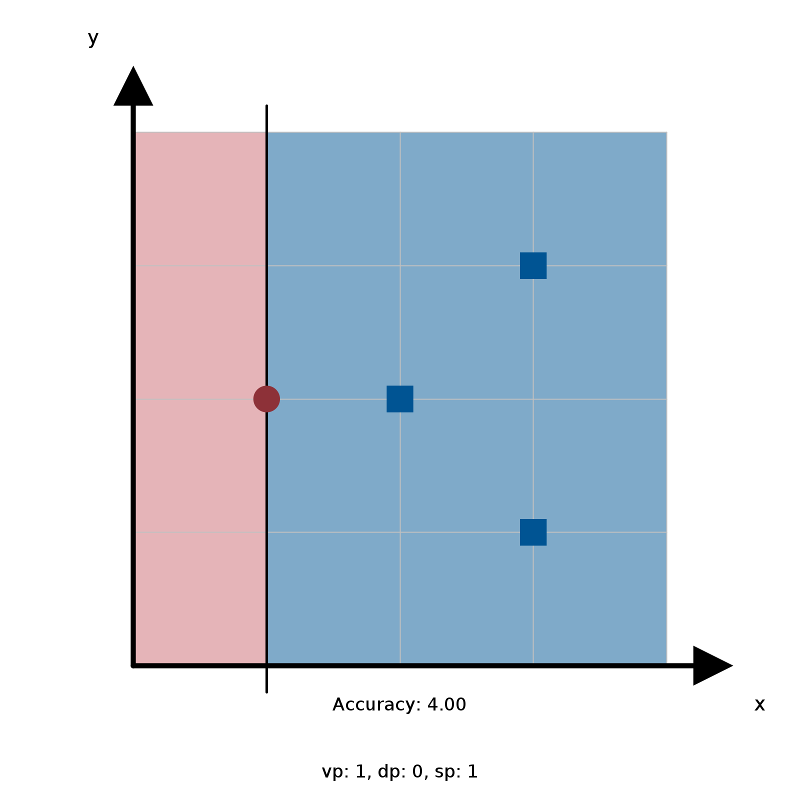
Example Visualizer

As you can tell from the image above, the client shows you the input points, the decision stump, the accuracy of the decision stump your implementation gets, as well as the values of \(d_p\), \(v_p\) and \(s_p\). To verify if you got the right answer, compare these values to the ones in stump_1.ans.txt.

Frequently Asked Questions (BoostingAlgorithm)

How do I normalize the weights and why do I have to? Normalizing can be done by summing all the weights and then dividing each individual weight by this sum. This ensures that the resulting weights sum to 1.

We do this because otherwise we might have problems with numeric overflow, since we are repeatedly doubling weights, if we never normalized, after 100 mistakes the weight of a point would be \(2^{100}\), which is larger than what a long can represent in java.

Why does this model work well to classify data? The intuition is that we are training several weak learners, each will be better at predicting certain collections of points. Individually, each weak learner is only slightly good at predicting, but when you combine all of them, they become really good.

Also, we must confess that in reality the exact model that you are implementing doesn't really work well for many scenarios. The complete AdaBoost algorithm is slightly more complex, and this extra complexity makes it work really well in all possible scenarios (one can even show theoretical guarantees on how well it works). We chose to have you learn and implement this simpler version to make your lives easier, but we encourage you to look up how the full version works and why.

Are there other types of weak learners? Certainly! Any simple model that is very efficient to train and predict, is a good candidate for a weak learner. The only thing you need is a model that is better than assigning labels at random. You are implementing decision stumps here because they are the simplest to understand and they are also really popular in practice.

Possible Progress Steps

These are purely suggestions for how you might make progress. You do not have to follow these steps.

  1. Implement all the methods in the Clustering data type. Go through the algorithm's description in the statement and think about what instance variables you'll need and what temporary variables you'll need in the constructor to compute them. Don't be wasteful! Only store as an instance variable what you really need to in order to support the instance methods.
  2. Implement all the methods in the WeakLearner data type using the \(O(kn^2)\) algorithm. Note that this data type is independent of Clustering, so you don't have to use that in this part of the assignment.
  3. Implement the BoostingAlgorithm data type. You'll need to create a single Clustering object in the constructor, and a WeakLearner every time the iterate() method gets called. Don't throw away these WeakLearners! Store them in a linked list or something like that, since you need them in the predict() method, to compute their predictions and take a majority.
  4. Once you got all of this to work and passed all tests on tigerfile except for one timing test on WeakLearner, try to find a \(O(nk \log n)\) solution and then implement it. Don't get rid of your inefficient solution, save it just in case you need to look at it again when you are trying to implement the more efficient one.

If you get stuck or confused, it might help to revisit the lecture slides and the precept exercises from Precept 10. Also, ask questions on Ed/go to office hours.