Fraud Detection

• Checklist
• Project
• Submit

In this assignment you are going to implement a few algorithms that, when put together, form a machine learning model to detect fraudulent credit card transactions. The model you will implement is a (very) simplified version of one that could be employed in the real world. In this process, you will apply many algorithms you learned throughout this course.

The base problem

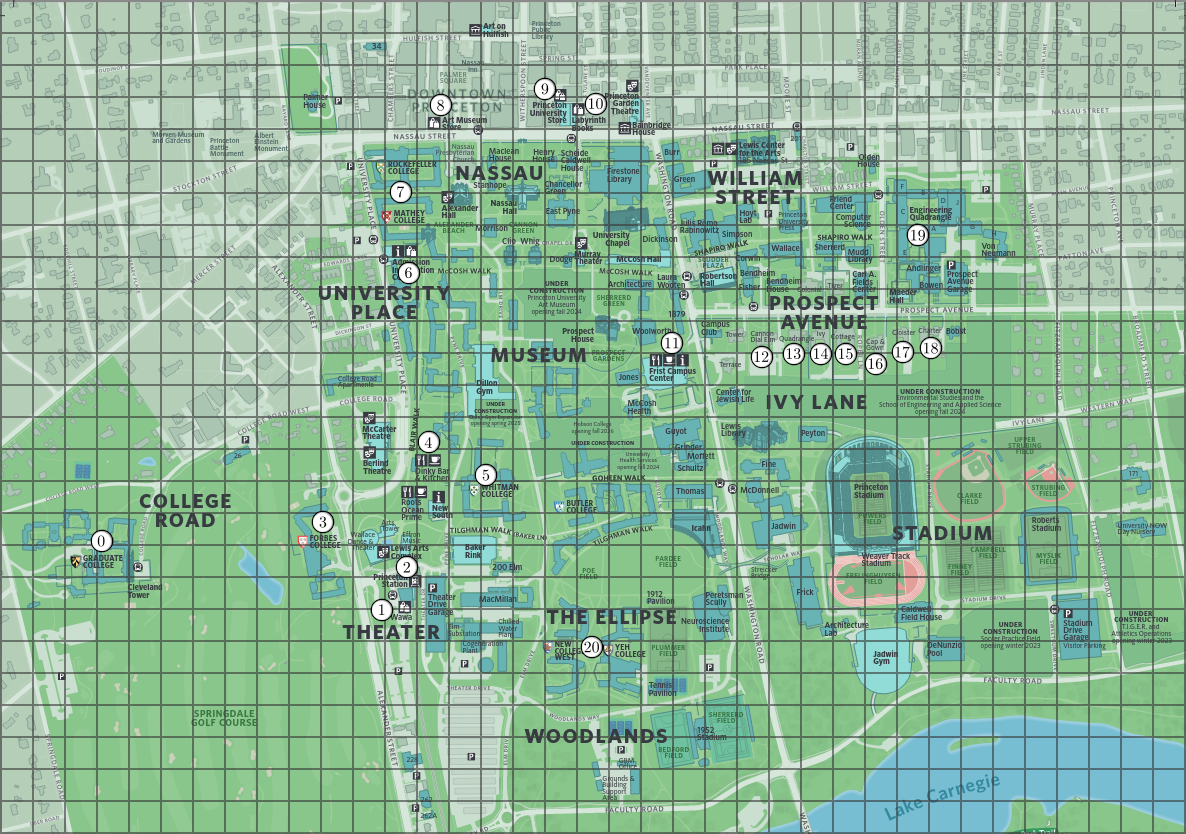
Consider a set of \(m\) points in 2D space, each representing coordinates of retail establishments, such as shops and restaurants, on a map. These points are represented using the immutable data type Point2D (part of algs4.jar). Below is an example of locations in a map of Princeton.

\(m = 21\) locations in Princeton (click to enlarge)

Additionally, you are given a data set with \(n\) labeled transaction summaries. In your implementation you can assume \(n\) is always at least 1. A transaction summary is an array of \(m\) non-negative numbers, one per location, representing the amount of money spent there using a particular credit card. A label is either clean or fraud, indicating whether a fraudulent transaction was detected in the corresponding transaction summary. Here is an example of one. Each number corresponds to a vertex in the graph (e.g. the first number represent the amount of money spent at "Graduate College," the leftmost point).

You will create a simple machine learning model that learns from this data set, in order to label new transaction summaries as either clean or Fraud. In your code you will represent these labels using integers, where \(0\) represents clean and \(1\) represents fraud.

Dimensionality reduction

Before feeding the data into the machine learning model, you will first reduce the dimension of the input using a clustering algorithm. This algorithm receives \(m\) objects of type Point2D (representing locations) as well as an integer \(k\), which represents the number of clusters (\(k\) should be at least 1 and at most \(m\)). The goal is to output a partition of the points into \(k\) clusters (i.e., groups), such that the points in the same cluster are similar (in our case, two points are similar if the Euclidean distance between them is small). Each cluster should be labeled by an integer between 0 and \(k - 1\). The output format is an array of \(k\) elements, the \(i\)th of which represents the total amount of money that transaction summary spent across all locations in the \(i\)th cluster.

This step is applied not only to make the model more efficient, but it also improves its accuracy by mitigating an overfit of the model to the input data.

Here is what the clustering algorithm should do:

• Create a complete edge weighted graph (using EdgeWeightedGraph) with \(m\) vertices (one per location on the map) and an edge connecting each pair of locations, weighted according to the Euclidean distance between the two points. The vertices should be numbered from \(0\) to \(m - 1\), in the order of the locations in the input.
• Compute the minimum spanning tree of the graph.
• Consider only the \(m - k\) edges with lowest weight of the spanning tree and form a new graph (the cluster graph) with them.
• Each cluster is now given by a connected component in this graph (note that the cluster graph has exactly \(k\) connected components).

You don't have to implement all these steps from scratch, there are several helpful classes in algs4.jar that you can use (see the implementation requirements below).

The following images represent the minimum spanning tree and the clusters obtained from the Princeton locations above, with \(k = 5\) groups/clusters. On the image on the right, the dashed lines represent the edges of the minimum spanning tree that are not in the new graph and the clusters are indicated by colors.

Minimum spanning tree and the \(k = 5\) clusters of the \(m = 21\) locations in the Princeton graph (click to enlarge)

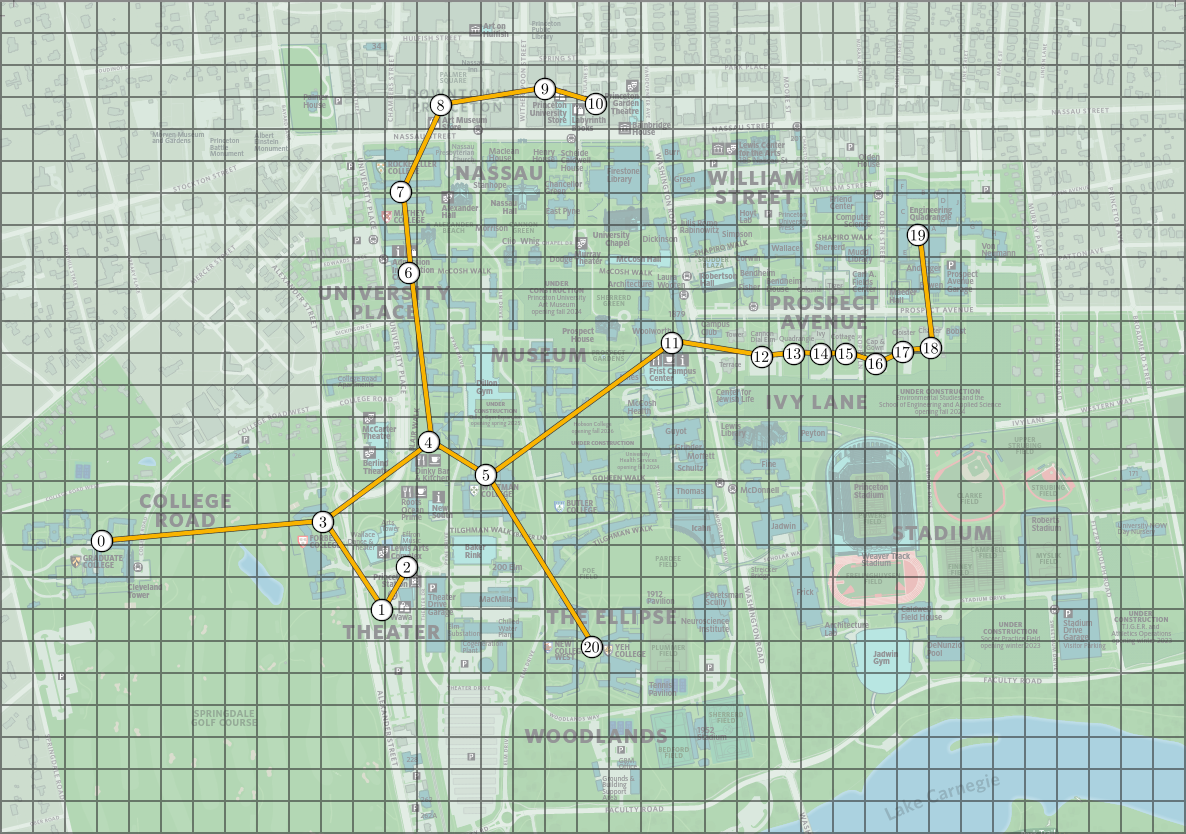
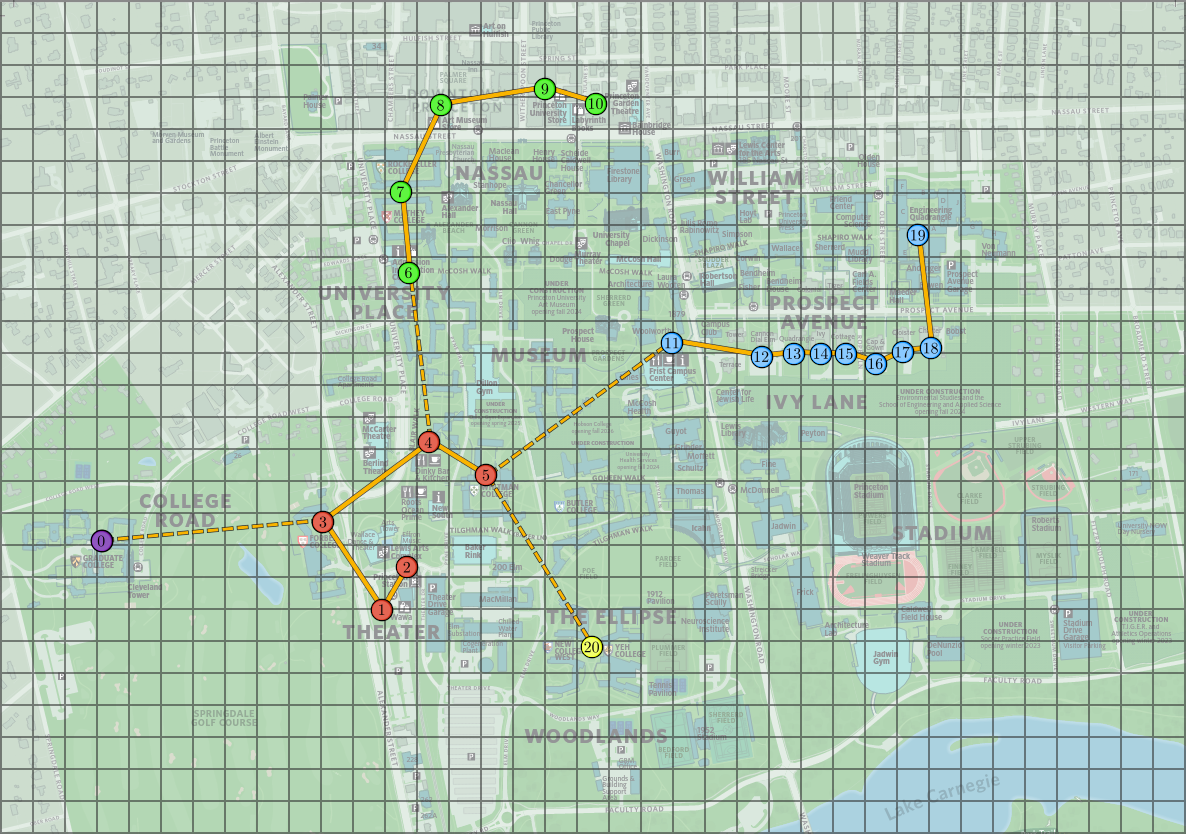
To help you test your code, we provide a file called princeton_locations.txt which starts with the number of locations and then contains one line per location, with the coordinates of the point. The points in this file follow the order of the above images (so again, the first point represent the "Graduate College," the leftmost one in the image). We also include a file princeton_locations_mst.txt that contains the edges of the minimum spanning tree of this graph.

With the clusters above, we can color the transaction summary by the corresponding cluster color and compute the array obtained by reducing its dimensions.

Clustering Algorithm. Write a class Clustering.java that implements the above clustering algorithm, by implementing the following API:

public class Clustering {

    // run the clustering algorithm and create the clusters  
    public Clustering(Point2D[] locations, int k)

    // return the cluster of the ith point 
    public int clusterOf(int i)

    // use the clusters to reduce the dimensions of an input 
    public double[] reduceDimensions(double[] input)

    // unit testing (required)
    public static void main(String[] args)
}

Note that the clusterOf() must return an integer between \(0\) and \(k-1\) and clusterOf(i) should only be equal to clusterOf(j) if and only if the \(i\)th and \(j\)th points are in the same cluster.

Implementation requirements.  You should use KruskalMST and CC to compute a minimum spanning tree and connected components.

Corner cases.  Throw an IllegalArgumentException if:

• any argument is null
• any element of an array argument is null
• \(k\) is less than \(1\) or more than \(m\)
• the argument of clusterOf() is not between \(0\) and \(m - 1\)
• the argument of reduceDimensions() has a length different from \(m\)

Unit testing.  Your main() method must call each public constructor and method directly and help verify that they work as prescribed (e.g., by printing results to standard output).

Performance requirements.  Your implementation must achieve the following performance requirements:

• clusterOf() should run in \(\Theta(1)\) time.
• The constructor should run in \(O(m^2 \log m)\) time.
• reduceDimensions() should run in \(O(m)\) time.

Weak learners

A weak learner is a machine learning model that performs marginally better than making random decisions. In the context of this assignment, this means predicting the right label more than \(50\%\) of the time. You will implement a model known as a decision stump, a really popular choice for weak learners.

A decision stump takes as input a sequence of \(n\) inputs, each represented by an array of \(k\) doubles (a dimension-reduced transaction summary). Each one of the inputs can be thought of as a point in \(k\)-dimensions. Each input is labeled with an integer, either \(0\) or \(1\) (corresponding to clean or fraud), which will be represented by an array of \(n\) integers. Additionally, each input also has a non-negative weight (this will be useful for the last part of the assignment), so weights are represented by an array of \(n\) doubles. From the input data and labels, the decision stump "learns" a predictor: a function that takes a single sample (i.e. any array of \(k\) doubles) as input and outputs a binary prediction, either \(0\) or \(1\) (i.e. clean or fraud).

To make a prediction the decision stump picks a (hyper)plane parallel to all of the axes except one and labels all points to one side of that plane as \(0\) and points on the other side as \(1\). To do so, the you need to compute three quantities: a dimension predictor \(d_p\), a value predictor \(v_p\) and a sign predictor \(s_p\).

The dimension predictor is an integer between \(0\) and \(k - 1\) that represents the non-parallel dimension/coordinate of the input space. The value predictor is a double that represents where the input space is partitioned (i.e. where the hyperplane crosses its non-parallel axis). The sign predictor is an integer, either \(0\) or \(1\), representing in which direction to partition space, i.e. which side of the plane gets labeled as \(0\) or \(1\).

When making a prediction on a input point \(sample\), if \(s_p = 0\) then the decision stump predicts \(0\) if \(sample[d_p] \leq v_p\) and \(1\) otherwise. But, if \(s_p = 1\) then the decision stump reverses the prediction: \(1\) if \(sample[d_p] \leq v_p\) and \(0\) otherwise.

The values of \(d_p\), \(v_p\) and \(s_p\) are chosen to maximize the weight of correctly classified inputs. This means maximizing the sum of the weights of the inputs such that their predicted label (according to the method of the above paragraph) matches the actual input label.

See the images below for an example with \(n = 8\) inputs of dimension \(k = 2\), where dimensions 0 and 1 correspond to the the x and y axes, respectively. For simplicity, in this example the weight of each point is \(1\). Blue squares correspond to the label \(0\) and red circles to the label \(1\). The best predictor is given by the line in the image on the right: points above the line are labeled as \(0\) and points on the line or below the line are labeled as \(1\).

Points on a grid and weak learner predictor (\(n = 8\), \(k = 2\)) (click to enlarge)
                 

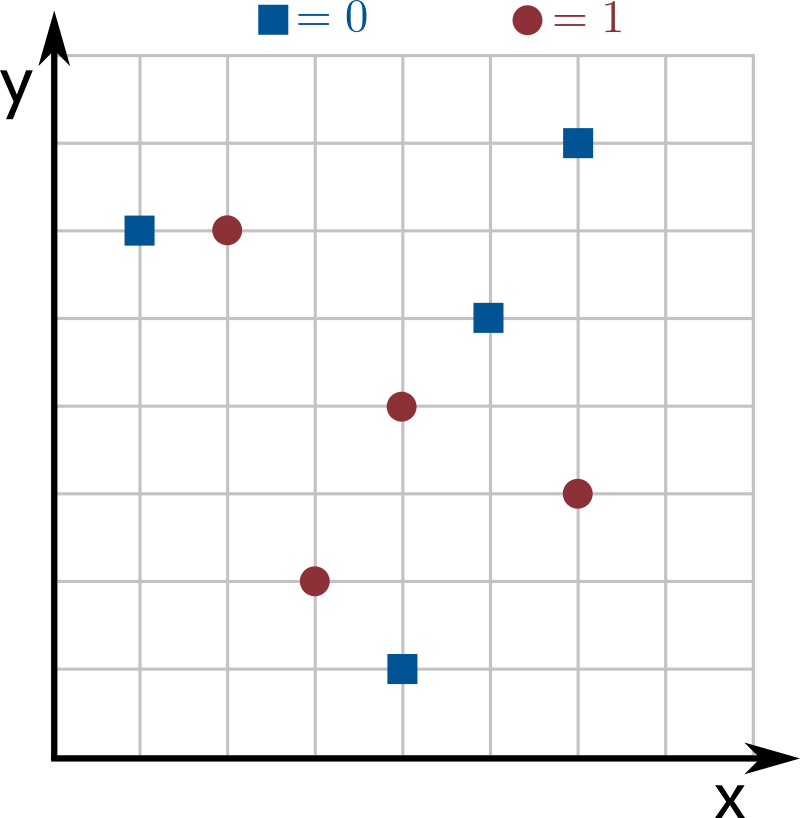
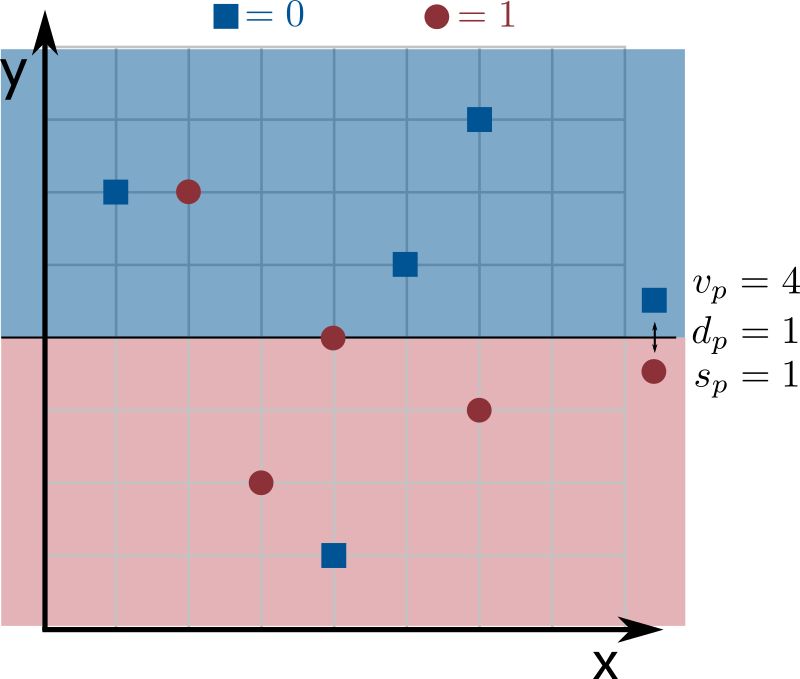
This weak learner mislabels two points, the top circle and the bottom square. Since no other weak learner mislabels less than 2 points, this one is optimal.

Weak Learner. Write a class WeakLearner.java that implements the above weak learner, by implementing the following API:

public class WeakLearner {

    // train the weak learner  
    public WeakLearner(double[][] input, double[] weights, int[] labels)

    // return the prediction of the learner for a new sample  
    public int predict(double[] sample)

    // return the dimension the learner uses to separate the data  
    public int dimensionPredictor()

    // return the value the learner uses to separate the data 
    public double valuePredictor()

    // return the sign the learner uses to separate the data 
    public int signPredictor()

    // unit testing (required)
    public static void main(String[] args)
}

Corner cases.  Throw an IllegalArgumentException if:

• any argument is null.
• the length of input, weights, labels or sample are incompatible.
• the values of weights are not all non-negative.
• the values of labels are not all either \(0\) or \(1\).

Unit testing.  We provide you with some code to help you test your WeakLearner.java implementation. See the section on "Testing the learners" below.

Performance requirements.  Your implementation must achieve the following performance requirements:

• dimensionPredictor(), valuePredictor(), signPredictor() and predict() should run in \(\Theta(1)\) time.
• The constructor should run in \(O(nk \log n)\) time. You will get 75% partial credit if your solution runs \(O(kn^2)\) time.

Boosting algorithm

As the name suggests, the weak learner is not a very interesting model. So you will implement a better one using a technique called boosting, which a term that describes algorithms that take weak learners and improve (boost) their quality. In this assignment you will implement a simplified version of an algorithm called AdaBoost (short for Adaptive Boosting), which is an application of the multiplicative weights algorithm.

The input is a sequence of \(n\) labeled transaction summaries, the \(m\) map locations, as well as an integer \(k\) representing the number of clusters to cluster the data into. You should start by creating a Clustering object so you can map transaction summaries into arrays of length \(k\), using the dimensionality reduction method. From now on we use the word input to refer to the reduced transaction summaries, i.e. the arrays resulting from applied the dimensionality reduction method to the original transaction summaries.

AdaBoost is a version of multiplicative weights where the input points are the experts. The algorithm assigns a weight to each input point, represented as a double array of length \(n\). This array is normalized, so that the sum of its elements is always \(1\). Initially, the weights should all be set to the same value: \(1 / n\).

The boosting algorithm works in steps or iterations. Each iteration should do the following:

• Create a weak learner using the current weights and the input.
• For each input point, double its weight if the weak learner you created mislabels it.
• Renormalize the weight array, so that it sums to \(1\) again.

We double the weight of mislabeled inputs to force the algorithm to try harder to predict them correctly in future iterations.

Given a sample to make a prediction on, the model should output the majority vote over the predictions given by the weak learner created in each iteration. This means you should use each weak learner created in each iteration to label the sample point, and then output the label that was predicted the most. In case of a tie, output \(0\).

Boosting Algorithm. Write a class BoostingAlgorithm.java that implements the above boosting algorithm, by implementing the following API:

public class BoostingAlgorithm {

    // create the clusters and initialize your data structures
    public BoostingAlgorithm(double[][] input, int[] labels, Point2D[] locations, int k)

    // return the current weights
    public double[] weights()

    // apply one step of the boosting algorithm 
    public void iterate()

    // return the prediction of the learner for a new sample 
    public int predict(double[] sample)

    // unit testing (required)
    public static void main(String[] args)
}

Corner cases.  Throw an IllegalArgumentException if:

• any argument is null.
• any element of an array argument is null.
• the length of input, labels, locations or sample are incompatible.
• \(k\) is less than \(1\) or more than \(m\).
• the values of labels are not all either \(0\) or \(1\).

Unit testing.  We provide you with some code to help you test your Boosting.java implementation. See the section on "Testing the learners" below.

Performance requirements.  Your implementation must achieve the following performance requirements:

• weights() should run in \(\Theta(1)\) time.
• predict() should call the WeakLearner's predict() method \(T\) times and the Clustering's reduceDimensions() method once, where \(T\) is the number of iterations done so far
• iterate() should create one WeakLearner object and then take \(O(n)\) time.
• The constructor should create a Clustering object and then run in \(O(nm)\) time.

Testing the learners

To help you test your programs, we provide a data type DataSet.java, whose constructor requires one string argument, a filename, and reads the contents of that file.

DataSet data type. The API of class DataSet.java provided to you:

public class DataSet {
    public int n, m;
    public Point2D[] locations;
    public double[][] input;
    public int[] labels;

    public DataSet(String filename)
}
	

A classical way of testing machine learning models is by partitioning labeled data into two data sets: a training and a test data set. The model is trained using the training data, and then it is tested on the test data set. We assess the quality of the model using a very simple metric called accuracy: the fraction of correct predictions. This metric can be used on the training, test or all inputs.

We provide several files that have been pre-partitioned into training and test data sets, named accordingly. Below is a sample client to test the BoostingAlgorithm.java model (we leave it up to you to modify it to work with the WeakLearner.java). It takes two filenames (training and test data set files), an integer \(k\) (the number of clusters for dimensionality reduction), and an integer \(T\) (the number of iterations of the boosting algorithm) as command-line arguments. It trains the model on the training data set and calculates the accuracy in the training and test data sets.

public static void main(String[] args) {
    // read in the terms from a file
    DataSet training = new DataSet(args[0]);
    DataSet test = new DataSet(args[1]);
    int k = Integer.parseInt(args[2]);
    int iterations = Integer.parseInt(args[3]);

    // train the model
    BoostingAlgorithm model = new BoostingAlgorithm(training.input, training.labels,
                                                        training.locations, k);
    for (int t = 0; t < iterations; t++)
        model.iterate();

    // calculate the training data set accuracy
    double trainingAccuracy = 0;
    for (int i = 0; i < training.n; i++)
        if (model.predict(training.input[i]) == training.labels[i])
            trainingAccuracy += 1;
    trainingAccuracy /= training.n;

    // calculate the test data set accuracy
    double testAccuracy = 0;
    for (int i = 0; i < test.n; i++)
        if (model.predict(test.input[i]) == test.labels[i])
            testAccuracy += 1;
    testAccuracy /= test.n;

    StdOut.println("Training accuracy of model: " + trainingAccuracy);
    StdOut.println("Test accuracy of model:     " + testAccuracy);
}

To help you test your code, we provide two data sets, one called princeton_training.txt and one called princeton_test.txt. Both use the locations from the map described in the beginning of the assignment, and the inputs and labels were generated using a simulation. Here are two example runs of the previous client with both models you implemented, and the expected output:

~/Desktop/fraud> java-algs4 WeakLearner princeton_training.txt princeton_test.txt
Training accuracy of model: 0.69125
Test accuracy of model:     0.67

~/Desktop/fraud> java-algs4 BoostingAlgorithm princeton_training.txt princeton_test.txt 5 100
Training accuracy of model: 0.92375
Test accuracy of model:     0.805

Note that the weak learner in the above test was trained with no dimensionality reduction (which is equivalent to setting \(k = m\)) and using uniform weights, that is, all weights are 1.

Information about the assignment

Submission.  Submit only Clustering.java, WeakLearner.java and BoostingAlgorithm.java. We will supply algs4.jar. You may not call library functions except those in those in java.lang, java.util, and algs4.jar. Finally, submit readme.txt and acknowledgments.txt files and answer the questions.

Grading.

file	points
Clustering.java	12
WeakLearner.java	12
BoostingAlgorithm.java	12
readme.txt	4
	40

Reminder: You can lose up to 4 points for poor style and up to 4 points for inadequate unit testing.