 Fraud Detection
Fraud Detection
Note: Since this is a new assignment, we might update this checklist if a lot of you ask us the same question (since it would be, literally, a frequently asked question).
What methods from Points2D can I use? You can
use any methods from its API, which you can consult
here Point2D. You
won't need most of the available methods, but you might want to use
the distanceTo() to compute Euclidean distances.
Do I have to implement both a minimum spanning tree and connected
components algorithm from scratch? No! You can use two data
types available in the algs4.jar, namely KruskalMST
and CC. The
first one let's you compute a minimum spanning tree and the second
one let's you compute connected components of a graph. Their APIs
are very short, so it should be easy to find what methods you need
to use.
What exactly is a cluster and why am I computing one? A cluster is a group of points that are close to each other. This is a very broad definition and in fact there are many reasonable ways of clustering points. We chose to use one based on minimum spanning trees so you can practice using this method you learned in class.
You are implementing something to compute clusters so you can reduce the dimension of the input by contracting all dimensions that are in the same cluster. This makes the classifier part of the algorithm more efficient, since you only have to deal with arrays of length \(k\), instead of length \(m\) (so if \(k\) is much smaller than \(m\), this is more efficient). Additionally, if you think about what the underlying machine learning model is doing, grouping together close locations is actually aggregating data in a useful way, so reducing dimensions in this way can actually help the model be better.
What is the best way to test my implementation? Once you have your weak learner implemented, the best way to test it is by first using the example in the provided image (which is reproduced below). Create a main method that sets up the input and label arrays according to these points, create a weights array with all elements equal to 1, and then train your weak learner. Then compare the value, dimension and sign predictors you obtained witht the correct ones.
When training a weak learner, how should I tie break over two weak learners with the same weight of correctly predicted points? The assignment doesn't specify, so it doesn't matter. For different data sets you might obtain a slightly different accuracy than the reference solution, but on the princeton_training.txt or princeton_test.txt examples you should obtain the same or a very similar accuracy.
If you are curious about our tie breaking rule, here is what the reference solution does: in case of a tie, always pick the smallest possible dimension predictor, if a tie still persists pick the smallest possible value predictor, and if a tie still yet persists, pick the smallest sign predictor.
I am not sure how to implement the constructor? This is probably the trickiest part of the assignment, so you might have to spend some time thinking about how to do this efficiently. Start by trying to get the less efficient \(O(kn^2)\) solution to work. To do it, notice that you can compute the weight of correct predictions for all possible weak learners. How? Try all possible values of \(d_p\) (there are \(k\) of them), all possible values of \(s_p\) (there are only 2 of them), and all values of \(v_p\), and compute the weight of correct predictions for each one of these weak learners (by looping through all \(n\) input points and computing the weak learner's prediction). But can't \(v_p\) be any possible non-negative value? Yes, but notice that we only care about values that are coordinates in our input (there are \(n\) of them). A weak learner with a value of \(v_p\) between two coordinates of our input does exactly the same predictions on our input, so its weight of correct predictions is the same. To visualize this, look at the example from the assignment statement:
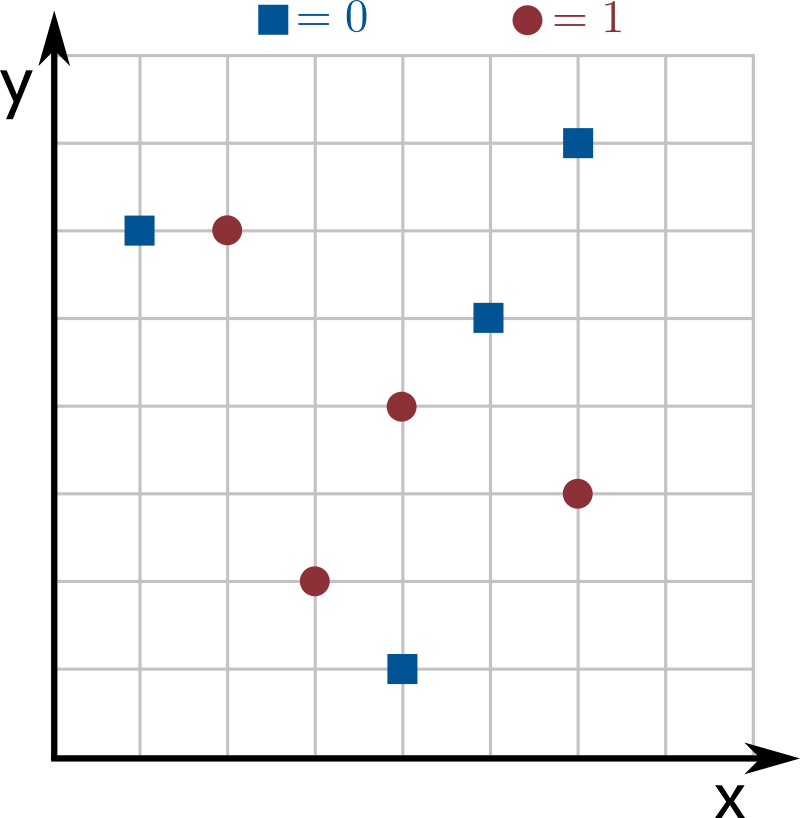
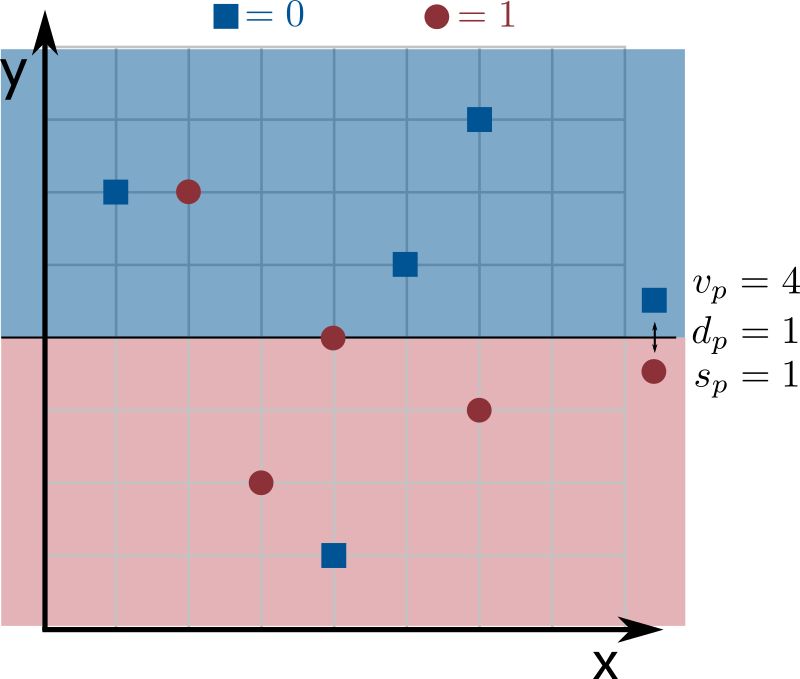
Note that moving the line up by anything less than \(1\) (so setting \(v_p\) to anything at least \(4\) and less than \(5\)) does the exact same predictions on the input.
Once you get this solution to work, think about how to avoid having to repeatedly go through all the points for every possible weak learner, by finding a more clever way to compute the weight of correct predictions without having to go through all points repeatedly. Hint: sorting might help here.
How do I normalize the weights and why do I have to? Normalizing can be done by summing all the weights and then dividing each individual weight by this sum. This ensures that the resulting weights sum to 1.
We do this because otherwise we might have problems with numeric
overflow, since we are repeatedly doubling weights, if we never
normalized, after 100 mistakes the weight of a point would be
\(2^{100}\), which is larger than what a long can
represent in java.
Why does this model work well to classify data? The intuition is that we are training several weak learners, each will be better at predicting certain collections of points. Individually, each weak learner is only slightly good at predicting, but when you combine all of them, they become really good.
Also, we must confess that in reality the exact model that you are implementing doesn't really work well for many scenarios. The complete AdaBoost algorithm is slightly more complex, and this extra complexity makes it work really well in all possible scenarios (one can even show theoretical guarantees on how well it works). We chose to have you learn and implement this simpler version to make your lives easier, but we encourage you to look up how the full version works and why.
Are there other types of weak learners? Certainly! Any simple model that is very efficient to train and predict, is a good candidate for a weak learner. The only thing you need is a model that is better than assigning labels at random. You are implementing decision stumps here because they are the simplest to understand and they are also really popular in practice.
These are purely suggestions for how you might make progress. You do not have to follow these steps.
Clustering data
type. Go through the algorithm's description in the statement and
think about what instance variables you'll need and what temporary
variables you'll need in the constructor to compute them. Don't be
wasteful! Only store as an instance variable what you really need
to in order to support the instance methods.WeakLearner data
type. Note that this data type is independent
of Clustering, so you don't have to use that in this
part of the assignment. It might be helpful to write unit tests to
train on the data points from the example in the image above, to
confirm you get the right answer.
BoostingAlgorithm data
type. You'll need to create a single Clustering
object in the constructor, and a WeakLearner every
time the iterate() method gets called. Don't throw
away these WeakLearners! Store them in a linked list
or something like that, since you need them in
the predict() method, to compute their predictions
and take a majority.
If you get stuck or confused, it might help to revisit the lecture slides and the precept exercises from Precept 10.