Programming Assignment 4: Arrays

The purpose of this assignment is to introduce you to programming with one-dimensional arrays.

Reverse sound wave. When an object vibrates, it creates a wave of air pressure, which we hear as sound. With digital audio, we model a sound wave as a sequence of audio samples. Each sample is a number between –1 and +1 that represents the change in pressure of the sound wave at a specific point in time. By sampling the sound wave many times per second, we can represent the sound accurately.
The StdAudio class uses a sampling rate of 44,100 Hz, which means that every second of digital audio contains 44,100 samples. You will use these two array-based functions for reading and playing audio samples:
- The function StdAudio.read(filename) returns a double[] array containing the samples (between –1 and +1) from the file specified as an argument.
- The function StdAudio.play(samples) sends the double[] array of samples to standard audio.
Write a program ReverseSoundWave.java that takes the name of an audio file as a command-line argument and plays it in reverse order. Your program should
- Read the audio samples from the audio file into an array using StdAudio.read().
- Reverse the elements in the array.
- Send that reversed array to standard audio using StdAudio.play().
Here are a few sample executions. Before running each example, make a prediction of what you think the reveresed audio will sound like.
```
~/Desktop/arrays> javac-introcs ReverseSoundWave.java
~/Desktop/arrays> java-introcs ReverseSoundWave A.wav



~/Desktop/arrays> java-introcs ReverseSoundWave AMajorScale.wav



~/Desktop/arrays> java-introcs ReverseSoundWave HelloWorld.wav



~/Desktop/arrays> java-introcs ReverseSoundWave ReverseHelloWorld.wav



~/Desktop/arrays> java-introcs ReverseSoundWave RowYourBoat.wav



~/Desktop/arrays> java-introcs ReverseSoundWave PacMan.wav
```
Playing music backward can sound creepy or demonic. On the other hand, playing a video backward is a popular effect on social media platforms such as TikTok.

Superposition of sound waves. A sound wave is a mechancial wave and is subject to the principle of superposition. This means that to combine two (or more) sound waves, you simply add the corresponding samples together. For example, to create a chord, superpose the sounds for the individual notes. To create a musical composition, superpose the sounds from the individual instruments or voices.

Write a program Superpose.java that reads a number of sound files (all of the same length) and plays the sound that results by superposing those sounds together. Your program should take the names of the sound files as command-line arguments.

~/Desktop/arrays> javac-introcs Superpose.java
~/Desktop/arrays> java-introcs Superpose SynthA.wav



~/Desktop/arrays> java-introcs Superpose SynthC#.wav



~/Desktop/arrays> java-introcs Superpose SynthE.wav



~/Desktop/arrays> java-introcs Superpose SynthA.wav SynthC#.wav SynthE.wav



~/Desktop/arrays> java-introcs Superpose TwinkleMelody.wav TwinkleHarmony.wav



~/Desktop/arrays> java-introcs Superpose PacMan1.wav PacMan2.wav



~/Desktop/arrays> java-introcs Superpose Bell1.wav Bell2.wav Bell3.wav



~/Desktop/arrays> java-introcs Superpose Crane1.wav Crane2.wav Crane3.wav Crane4.wav



~/Desktop/arrays> java-introcs Superpose InvertedSynthA.wav



~/Desktop/arrays> java-introcs Superpose SynthA.wav InvertedSynthA.wav

The Chipmunk Effect. In this exercise, we will speed up a sound file by resampling it, at a rate \(\alpha > 1\), which results in faster. In turn, this will raise the pitch of the sound and lead to the classic Chipmunk effect.
The resampling works as follows: If the existing sound has \(n\) samples, then the new sound will have \(\lfloor n / \alpha\rfloor\) samples, and sample \(i\) of the new sound corresponds to sample \(\lfloor\alpha \cdot i\rfloor\) of the existing sound (both assume zero-indexing, i.e., that the first entry of the array corresponds to \(i = 0\)). As a reminder, the floor function \(\lfloor x \rfloor\) returns the largest integer less than or equal to \(x\). You can compute this function in Java by casting x to an integer or by calling Math.floor(x).
Write a program ChipmunkEffect.java that takes two command-line arguments: a string filename and a double alpha. Your program should change the speed of the sound specified by the filename, and play the resampled sound.

Here are some sample executions:
```
~/Desktop/arrays> javac-introcs ChipmunkEffect.java
~/Desktop/arrays> java-introcs ChipmunkEffect KevinWayne.wav 1.0



~/Desktop/arrays> java-introcs ChipmunkEffect KevinWayne.wav 1.5



~/Desktop/arrays> java-introcs ChipmunkEffect SebastianCaldas.wav 1.0



~/Desktop/arrays> java-introcs ChipmunkEffect SebastianCaldas.wav 1.7
```
This type of filter is a popular voice effect that you can apply on social media platforms such as TikTok.
Perfect shuffle. There are many techniques for shuffling a deck of playing cards. In a riffle shuffle, the dealer divides (cuts) the deck into two (roughly) equal piles and then the cards in the two piles are (approximately) interleaved back together. A perfect out-shuffle (or Faro shuffle) is an idealized version of this in which the deck is cut exactly in half and the cards in the two halves are perfectly interleaved back together, leaving the original top card on the top and the original bottom card on the bottom.
For example, the following illustrates a perfect shuffle of an 8-card deck:

Amazingly, after perfectly shuffling a 52-card deck 8 times, the deck returns to its original order!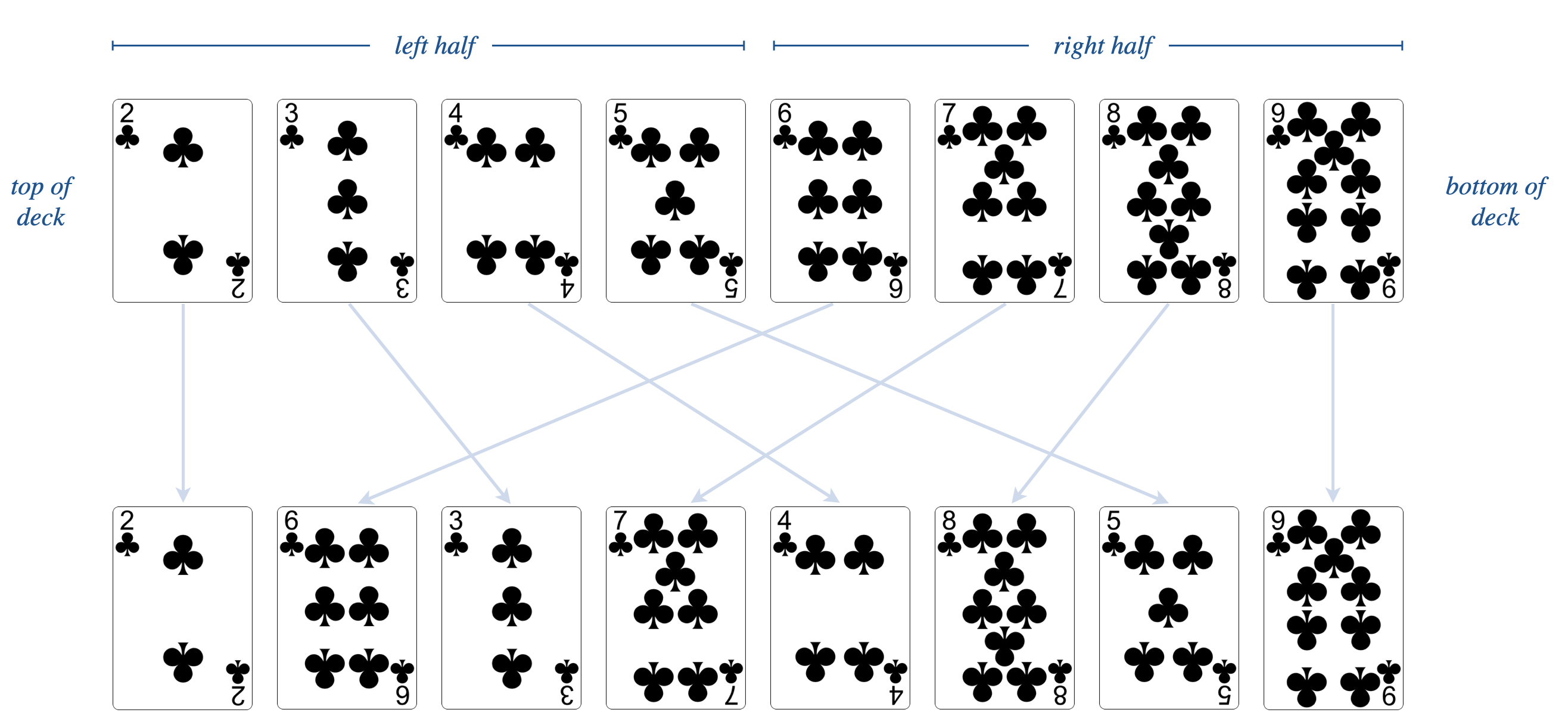
Write a program PerfectShuffle.java that takes two integer command-line arguments \(m\) and \(n\), initializes a deck of \(m\) cards, applies \(n\) perfect shuffles to the deck, and prints the results.
- Represent each card as a string, using one character for the rank (2, 3, 4, 5, 6, 7, 8, 9, T, J, Q, K, A) followed by one character for the suit (C, D, H, S). For example, 2C is the two of clubs and QH is the queen of hearts.
- Assume that the initial deck is sorted by suit, then rank; so the first card is 2C, the second is 3C, the 13^th (if \(m \geq 13\)) is 2D and the last (if \(m = 52\)) is AS.
More precisely, on input m n, you must:
1. Create an array of length \(m\) that consists of the first \(m\) cards in sorted order.
2. Repeat the following \(n\) times:
3. Print the cards in the order thus obtained.
Here are some sample executions:
```
~/Desktop/arrays> javac-introcs PerfectShuffle.java
~/Desktop/arrays> java-introcs PerfectShuffle 8 0
2C 3C 4C 5C 6C 7C 8C 9C
~/Desktop/arrays> java-introcs PerfectShuffle 8 1
2C 6C 3C 7C 4C 8C 5C 9C
~/Desktop/arrays> java-introcs PerfectShuffle 8 2
2C 4C 6C 8C 3C 5C 7C 9C
~/Desktop/arrays> java-introcs PerfectShuffle 8 3
2C 3C 4C 5C 6C 7C 8C 9C
~/Desktop/arrays> java-introcs PerfectShuffle 52 4
2C 5D 8H JS 2D 5H ... JD AH 5C 8D JH AS
~/Desktop/arrays> java-introcs PerfectShuffle 52 8
2C 3C 4C 5C 6C 7C ... 9S TS JS QS KS AS
```
The perfect shuffle is useful in parallel processing algorithms, including the fast Fourier transform (which is widely used in science, engineering, and music). It is also used by magicians and card cheats.

Submission. Submit ReverseSoundWave.java, Superpose.java, ChipmunkEffect.java, and PerfectShuffle.java. Also submit a readme.txt file and answer the questions. Do not use Java features that have not yet been introduced in the course (such as functions).

Grading.

File Points

ReverseSoundWave.java 9

Superpose.java 9

ChipmunkEffect.java 9

PerfectShuffle.java 9

readme.txt 4

Total 40

This assignment was developed by Sebastian Caldas, Marcel Dall'Agnol and Kevin Wayne. The Reverse and Superposition exercises were based on Song Generator by Daniel Zingaro. The Chipmunk Effect exercise is based on the changeSpeed() function from Princeton's Conjunction Function assignment.
Copyright © 2024.
Credits.

File	Points
ReverseSoundWave.java	9
Superpose.java	9
ChipmunkEffect.java	9
PerfectShuffle.java	9
readme.txt	4
Total	40