WordNet is a semantic lexicon for the English language that computational linguists and cognitive scientists use extensively. For example, WordNet was a key component in IBM’s Jeopardy-playing Watson computer system. WordNet groups words into sets of synonyms called synsets. For example, { AND circuit, AND gate } is a synset that represent a logical gate that fires only when all of its inputs fire. WordNet also describes semantic relationships between synsets. One such relationship is the is-a relationship, which connects a hyponym (more specific synset) to a hypernym (more general synset). For example, the synset { gate, logic gate } is a hypernym of { AND circuit, AND gate } because an AND gate is a kind of logic gate.

The WordNet digraph. Your first task is to build the WordNet digraph: each vertex v is an integer that represents a synset, and each directed edge v→w represents that w is a hypernym of v. The WordNet digraph is a rooted DAG: it is acyclic and has one vertex—the root—that is an ancestor of every other vertex. However, it is not necessarily a tree because a synset can have more than one hypernym. Here is a small subgraph of the WordNet digraph:

The WordNet input file formats. We now describe the two data files that you will use to create the WordNet digraph. The files are in comma-separated values (CSV) format: each line contains a sequence of fields, separated by commas.

WordNet data type. Implement an immutable data type WordNet with the following API: 

public class WordNet {

   // constructor takes the name of the two input files
   public WordNet(String synsets, String hypernyms)

   // the set of all WordNet nouns
   public Iterable<String> nouns()

   // is the word a WordNet noun?
   public boolean isNoun(String word)

   // a synset (second field of synsets.txt) that is a shortest common ancestor
   // of noun1 and noun2 (defined below)
   public String sca(String noun1, String noun2)

   // distance between noun1 and noun2 (defined below)
   public int distance(String noun1, String noun2)

   // unit testing (required)
   public static void main(String[] args)

}
Corner cases.  Throw an IllegalArgumentException in the following situations: You may assume that the input files are in the specified format and that the underlying digraph is a rooted DAG.

Unit testing.  Your main() method must call each public constructor and method directly and help verify that they work as prescribed (e.g., by printing results to standard output).

Performance requirements.  Your implementation must achieve the following performance requirements. In the requirements below, assume that the number of characters in a noun or synset is bounded by a constant.

Shortest common ancestor. An ancestral path between two vertices v and w in a rooted DAG is a directed path from v to a common ancestor x, together with a directed path from w to the same ancestor x. A shortest ancestral path is an ancestral path of minimum total length. We refer to the common ancestor in a shortest ancestral path as a shortest common ancestor. Note that a shortest common ancestor always exists because the root is an ancestor of every vertex. Note also that an ancestral path is a path, but not a directed path.

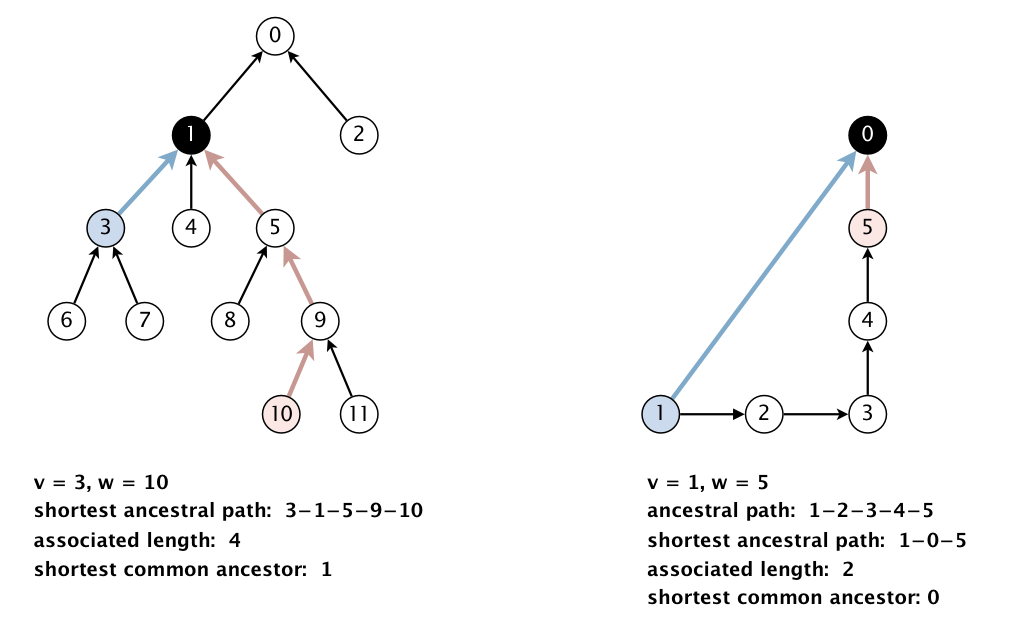
We generalize the notion of shortest common ancestor to subsets of vertices. A shortest ancestral path of two subsets of vertices A and B is a shortest ancestral path among all pairs of vertices v and w, with v in A and w in B. As an example, the following figure (digraph25.txt) identifies several (but not all) ancestral paths between the red and blue vertices, including the shortest one.


Shortest common ancestor data type. Implement an immutable data type ShortestCommonAncestor with the following API: 

public class ShortestCommonAncestor {

   // constructor takes a rooted DAG as argument
   public ShortestCommonAncestor(Digraph G)

   // length of shortest ancestral path between v and w
   public int length(int v, int w)

   // a shortest common ancestor of vertices v and w
   public int ancestor(int v, int w)

   // length of shortest ancestral path of vertex subsets A and B
   public int lengthSubset(Iterable<Integer> subsetA, Iterable<Integer> subsetB)

   // a shortest common ancestor of vertex subsets A and B
   public int ancestorSubset(Iterable<Integer> subsetA, Iterable<Integer> subsetB)

   // unit testing (required)
   public static void main(String[] args)

}

Corner cases.  Throw an IllegalArgumentException in the following situations:

Unit testing.  Your main() method must call each public constructor and method directly and help verify that they work as prescribed (e.g., by printing results to standard output).

Basic performance requirements.  Your implementation must achieve the following worst-case performance requirements, where E and V are the number of edges and vertices in the digraph, respectively.

Additional performance requirements (for extra credit).  In addition, the methods length(), lengthSubset(), ancestor(), and ancestorSubset() must take time proportional to the number of vertices and edges reachable from the argument vertices (or better), For example, to compute the shortest common ancestor of v and w in the following digraph, your algorithm can examine only the highlighted vertices and edges; it cannot initialize any vertex-indexed arrays.

Test client. The following test client takes the name of a digraph input file as as a command-line argument; creates the digraph; reads vertex pairs from standard input; and prints the length of the shortest ancestral path between the two vertices, along with a shortest common ancestor: 

public static void main(String[] args) {
    In in = new In(args[0]);
    Digraph G = new Digraph(in);
    ShortestCommonAncestor sca = new ShortestCommonAncestor(G);
    while (!StdIn.isEmpty()) {
        int v = StdIn.readInt();
        int w = StdIn.readInt();
        int length   = sca.length(v, w);
        int ancestor = sca.ancestor(v, w);
        StdOut.printf("length = %d, ancestor = %d\n", length, ancestor);
    }
}
Here is a sample execution (the yellow text indicates what you type): 
~/Desktop/wordnet> more digraph1.txt
12
11
 6  3
 7  3
 3  1
 4  1
 5  1
 8  5
 9  5
10  9
11  9
 1  0
 2  0

~/Desktop/wordnet> java-algs4 ShortestCommonAncestor digraph1.txt
3 10
length = 4, ancestor = 1
8 11
length = 3, ancestor = 5
6 2
length = 4, ancestor = 0

Measuring the semantic relatedness of two nouns. Semantic relatedness refers to the degree to which two concepts are related. Measuring semantic relatedness is a challenging problem. For example, you consider George W. Bush and John F. Kennedy (two U.S. presidents) to be more closely related than George W. Bush and chimpanzee (two primates). It might not be clear whether George W. Bush and Eric Arthur Blair are more related than two arbitrary people. However, both George W. Bush and Eric Arthur Blair (a.k.a. George Orwell) are famous communicators and, therefore, closely related.

We define the semantic relatedness of two WordNet nouns x and y as follows:

This is the notion of distance that you will use to implement the distance() and sca() methods in the WordNet data type.

Outcast detection. Given a list of WordNet nouns x1, x2, ..., xn, which noun is the least related to the others? To identify an outcast, compute the sum of the distances between each noun and every other one:

di   =   distance(xi, x1)   +   distance(xi, x2)   +   ...   +   distance(xi, xn)
and return a noun xt for which dt is maximum. Note that distance(xi, xi) = 0, so it will not contribute to the sum.

Implement an immutable data type Outcast with the following API: 

public class Outcast {

   // constructor takes a WordNet object
   public Outcast(WordNet wordnet)

   // given an array of WordNet nouns, return an outcast
   public String outcast(String[] nouns)

   // test client (see below)
   public static void main(String[] args)

}

Corner cases. Assume that the argument to outcast() contains only valid WordNet nouns and that it contains at least two such nouns.

Test client. The following test client takes from the command line the name of a synset file, the name of a hypernym file, followed by the names of outcast files, and prints an outcast in each file: 

public static void main(String[] args) {
    WordNet wordnet = new WordNet(args[0], args[1]);
    Outcast outcast = new Outcast(wordnet);
    for (int t = 2; t < args.length; t++) {
        In in = new In(args[t]);
        String[] nouns = in.readAllStrings();
        StdOut.println(args[t] + ": " + outcast.outcast(nouns));
    }
}
Here is a sample execution: 
~/Desktop/wordnet> more outcast5.txt
horse zebra cat bear table

~/Desktop/wordnet> more outcast8.txt
water soda bed orange_juice milk apple_juice tea coffee

~/Desktop/wordnet> more outcast11.txt
apple pear peach banana lime lemon blueberry strawberry mango watermelon potato

~/Desktop/wordnet> java-algs4 Outcast synsets.txt hypernyms.txt outcast5.txt outcast8.txt outcast11.txt
outcast5.txt: table
outcast8.txt: bed
outcast11.txt: potato

Analysis of running time. Analyze the potential effectiveness of your approach to this problem by answering the following questions:

Give your answers as a function of the number of vertices V and the number of edges E in the digraph.

Deliverables. Submit WordNet.java, ShortestCommonAncestor.java, and Outcast.java. Also submit any other supporting files (excluding those in algs4.jar). You may not call any library functions other than those in java.lang, java.util, and algs4.jar. Finally, submit a readme.txt file and answer the questions.

Grading.

file points
WordNet.java 14
ShortestCommonAncestor.java 14
Outcast.java 6
readme.txt 6
40

Reminder: You can lose up to 4 points for poor style and up to 4 points for inadequate unit testing.

Extra credit: You can earn 1–3 bonus points for meeting the additional performance requirements.

This assignment was created by Alina Ene and Kevin Wayne.
Copyright © 2006.