
What are the main goals of this assignment?
What preparation do I need before beginning this assignment? Read Section 4.3. Pay particular attention to the parts that deal with linked lists.
Can I program with a partner on this assignment? Yes. You are encouraged (not required) to work with a partner provided you practice pair programming.
Do I need to follow the prescribed API? Yes, we will be testing the methods in the API directly. If your method has a different signature or does not behave as specified, you will lose a substantial number of points. You may not add public methods to the API; however, you may add private methods (which are accessible from only the class in which they are declared).
What should the various methods do if the tour has no points? The size() method should return 0; the length() method should return 0.0; the toString() method should return the empty string; the draw() method should draw nothing to standard drawing.
How do I represent infinity in Java? Use Double.POSITIVE_INFINITY.
How can I produce an animation of the heuristic in action? It's easy and instructive—just redraw the tour after each insertion. See the instructions in SmallestInsertion.java. It could take a while on a big input file, so you might want to modify it so that it redraws only after every 20 insertions or so. Note: when timing your program, don't show the animation or else this may become the bottleneck.
What is the file Tour$Node.class?When you declare a nested class like Node, the Java compiler uses the $ symbol to mark its name.
How can the suggested definition of private class Node work when it has no constructor declared? If you do not declare a constructor, Java automatically defines a no-argument constructor that sets all of the instance variables to their default values (here null since Point and Node are reference types).
What is a NullPointerException? You can get one by initializing a variable of type Node, say x, to null and then accessing x.next or x.p. This can happen in your insertion routine if you inadvertently break up the circularly linked list.
When should I create a new linked-list node with the keyword new? To create a tour with n points, you should use new exactly n times with Node, once per invocation of insert(). It is unnecessary (and bad style) to use new with your list-traversal variables since this allocates memory that you never use.
When I run TSPTimer.java, I get inconsistent timing results. How can I fix this?
When I run TSPTimer.java with 10,000 points, it already takes more than a minute. What should I do? You have a performance error. Try to discover why (think analysis of algorithms) and explain it in your readme.txt file.
When I run TSPTimer.java with 10,000 points, my nearest insertion heuristic runs quickly, but my smallest insertion heuristic takes forever. How can I fix this? You probably have a loop that looks at inserting the new point at each possible insertion point. That is fine. However, if you are calling the length() method to compute the new tour length at each potential insertion point, you are effectively adding a second loop inside your first loop (even though it is a single method call), which is too slow. You do not need to recompute the entire tour length for each possible insertion point. Instead, compute the change in the tour length and keep track of which insertion point results in the smallest such change.
Can I use Java's built in LinkedList class? Absolutely not! One of the goals of this assignment is to gain experience writing and using linked structures. The Java libraries can take you only so far, and you will quickly discover applications which cannot be solved without devising your own linked structures.
Must I use a circularly linked list for the leaderboard? No, you are not required to use the Tour data type or linked lists for the leaderboard. Of course, you should exercise good modular design.
Input. The files for this assignment include many sample inputs. Most are taken from TSPLIB.
Debugging. A good debugging strategy for most programs is to test your code on inputs that you can easily solve by hand. Start with 1- and 2-point problems. Then, do a 4-point problem. Choose the data so that it is easy to work through the code by hand. Draw pictures. If your code does not do exactly what your hand calculations indicate, determine where they differ. Use the StdOut.println() method to trace.
Checking your work. For usa13509.txt we get tour lengths of 77449.9794 and 45074.7769 for nearest insertion and smallest insertion, respectively. For circuit1290.txt we get 25029.7905 and 14596.0971.
Timing. You may use the client program TSPTimer.java to help you estimate the running time as a function of the input size n. It takes a command-line argument n, runs the two heuristics on a random input of size n, and prints how long each took.
% java-introcs -Xint TSPTimer 1000 Tour length = 26338.42949015926 Nearest insertion: 0.056 seconds Tour length = 15505.745750759515 Smallest insertion: 0.154 seconds
The -Xint flag turns off various compiler optimizations, which helps normalize and stabilize the timing data that you collect.
Static visualizer. Use the clients NearestInsertion.java and SmallestInsertion.java, as descried in the assignment specification.
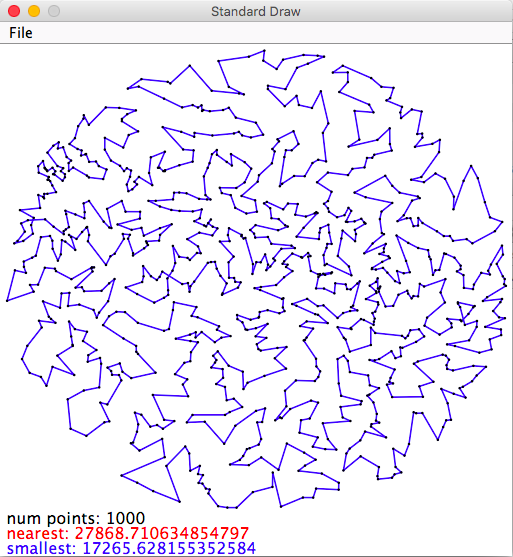
Interactive visualizer. TSPVisualizer.java in an interactive TSP visualizer. When you click a point in the window, it will add it to your tour. It displays both the nearest neighbor heuristic tour (in red) and the smallest insertion heuristic (in blue). You can toggle the visibility of the two tours by typing n (for nearest neighbor) or s (for smallest insertion).
% java-introcs TSPVisualizer tsp1000.txt |
|
 |
 |
If you want to test Tour.java after implementing only one of the insertion methods, you must declare the other method (even if it does nothing).
These are purely suggestions for how you might make progress. You do not have to follow these steps.
To test the size() method, write a main() method that defines four points, constructs a new Tour object using those four points, and calls its size() method.
public static void main(String[] args) {
// define 4 points that are the corners of a square
Point a = new Point(100.0, 100.0);
Point b = new Point(500.0, 100.0);
Point c = new Point(500.0, 500.0);
Point d = new Point(100.0, 500.0);
// create the tour a -> b -> c -> d -> a
Tour squareTour = new Tour(a, b, c, d);
// print the size to standard output
int size = squareTour.size();
StdOut.println("Number of points = " + size);
}
Test the length() method on the 4-point tour—the length should be 1600.0.
// print the tour length to standard output
double length = squareTour.length();
StdOut.println("Tour length = " + length);
Test the toString() method on the 4-point tour.
// print the tour to standard output
StdOut.println(squareTour);
You should get the following output:
(100.0, 100.0) (500.0, 100.0) (500.0, 500.0) (100.0, 500.0)
StdDraw.setXscale(0, 600); StdDraw.setYscale(0, 600);to resize the x- and y-coordinates of standard drawing.
Test the draw() method on the 4-point tour—you should see a square.