WordNet

• Checklist
• Project
• Submit
• Leaderboard

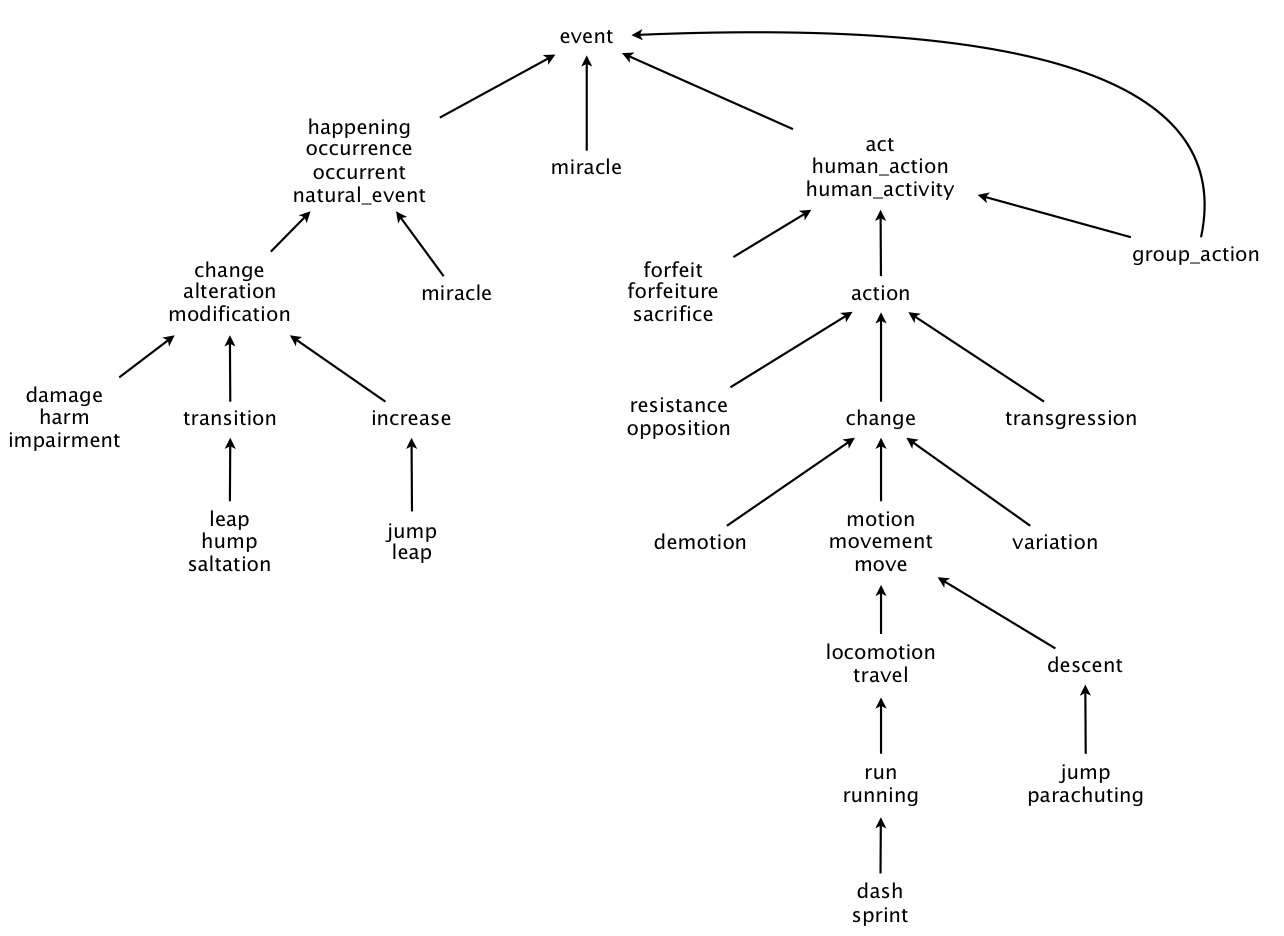
The WordNet digraph. Your first task is to build the WordNet digraph: each vertex v is an integer that represents a synset, and each directed edge v→w represents that w is a hypernym of v. The WordNet digraph is a rooted DAG: it is acyclic and has one vertex—the root—that is an ancestor of every other vertex. However, it is not necessarily a tree because a synset can have more than one hypernym. Here is a small subgraph of the WordNet digraph:

The WordNet input file formats. We now describe the two data files that you will use to create the WordNet digraph. The files are in comma-separated values (CSV) format: each line contains a sequence of fields, separated by commas.

• List of synsets. The file synsets.txt contains all noun synsets in WordNet, one per line. Line i of the file (counting from 0) contains the information for synset i. The first field is the synset id, which is always the integer i; the second field is the synonym set (or synset); and the third field is its dictionary definition (or gloss), which is not relevant to this assignment (and so you can ignore it).
  
  For example, line 36 means that the synset { AND_circuit, AND_gate } has an id number of 36 and its gloss is a circuit in a computer that fires only when all of its inputs fire. The individual nouns that constitute a synset are separated by spaces. If a noun contains more than one word, the underscore character connects the words (and not the space character).
• List of hypernyms. The file hypernyms.txt contains the hypernym relationships. Line i of the file (counting from 0) contains the hypernyms of synset i. The first field is the synset id, which is always the integer i; subsequent fields are the id numbers of the synset’s hypernyms.
  
  For example, line 36 means that synset 36 (AND_circuit AND_Gate) has 43273 (gate logic_gate) as its only hypernym. Line 34 means that synset 34 (AIDS acquired_immune_deficiency_syndrome) has two hypernyms: 48504 (immunodeficiency) and 49019 (infectious_disease).

WordNet data type. Implement an immutable data type WordNet with the following API:

public class WordNet {

   // constructor takes the name of the two input files
   public WordNet(String synsets, String hypernyms)

   // the set of all WordNet nouns
   public Iterable<String> nouns()

   // is the word a WordNet noun?
   public boolean isNoun(String word)

   // a synset (second field of synsets.txt) that is a shortest common ancestor
   // of noun1 and noun2 (defined below)
   public String sca(String noun1, String noun2)

   // distance between noun1 and noun2 (defined below)
   public int distance(String noun1, String noun2)

   // unit testing
   public static void main(String[] args)

}

Corner cases.  Throw an IllegalArgumentException in the following situations:

• Any argument to the constructor or an instance method is null
• Any of the noun arguments in distance() or sca() is not a WordNet noun.

Unit testing.  You don't need to create unit tests. Use the examples in the Checklist to help you test your implementation.

Performance requirements.  Your implementation must achieve the following performance requirements. In the requirements below, assume that the number of characters in a noun or synset is bounded by a constant.

• Your data type must use space linear in the input size (size of synsets and hypernyms files).
• The constructor must take time linearithmic (or better) in the input size.
• The method isNoun() must run in time logarithmic (or better) in the number of nouns.
• The methods distance() and sca() must make exactly one call to the lengthSubset() and ancestorSubset() methods in ShortestCommonAncestor, respectively.

Shortest common ancestor. An ancestral path between two vertices v and w in a rooted DAG is a directed path from v to a common ancestor x, together with a directed path from w to the same ancestor x. A shortest ancestral path is an ancestral path of minimum total length. We refer to the common ancestor in a shortest ancestral path as a shortest common ancestor. Note that a shortest common ancestor always exists because the root is an ancestor of every vertex. Note also that an ancestral path is a path, but not a directed path.

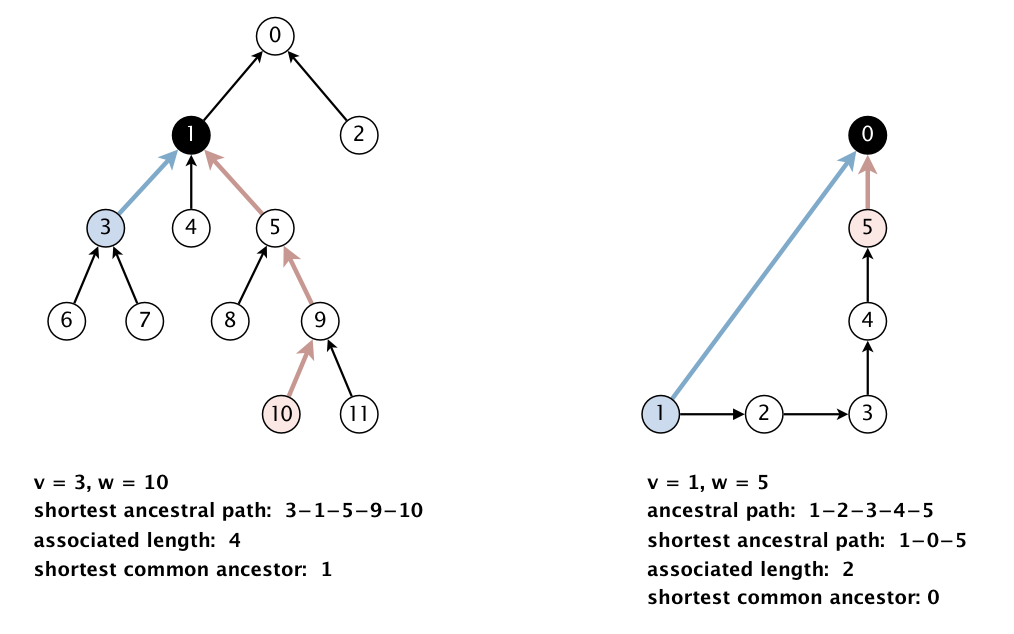
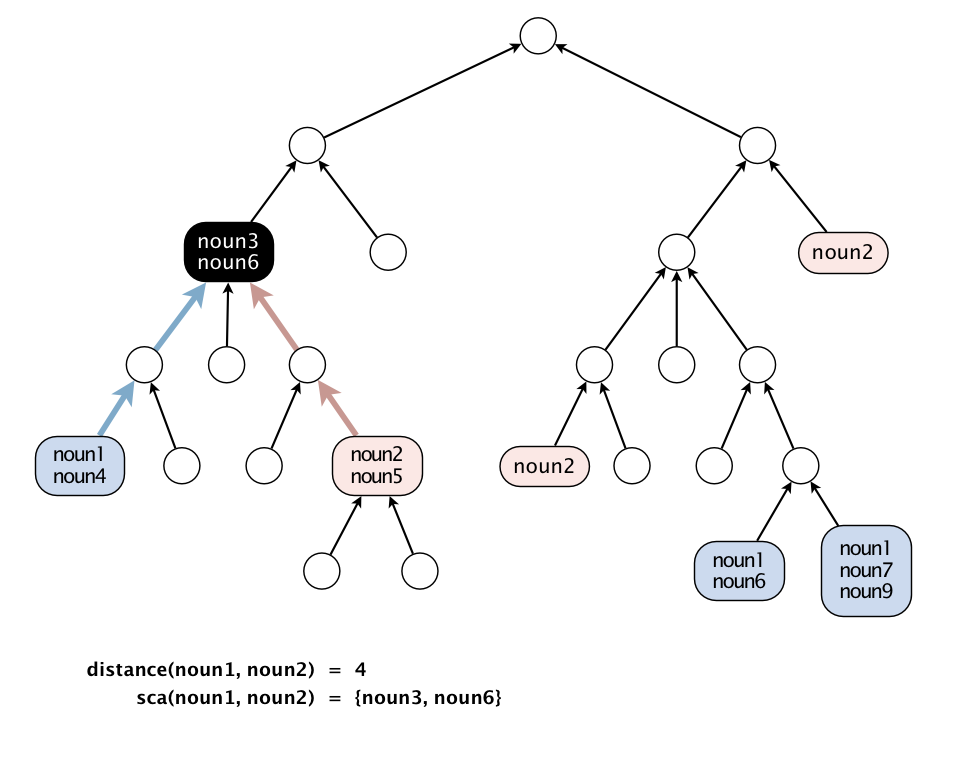
We generalize the notion of shortest common ancestor to subsets of vertices. A shortest ancestral path of two subsets of vertices A and B is a shortest ancestral path among all pairs of vertices v and w, with v in A and w in B. As an example, the following figure (digraph25.txt) identifies several (but not all) ancestral paths between the red and blue vertices, including the shortest one.

Shortest common ancestor data type. Implement an immutable data type ShortestCommonAncestor with the following API:

public class ShortestCommonAncestor {

   // constructor takes a rooted DAG as argument
   public ShortestCommonAncestor(Digraph G)

   // length of shortest ancestral path between v and w
   public int length(int v, int w)

   // a shortest common ancestor of vertices v and w
   public int ancestor(int v, int w)

   // length of shortest ancestral path of vertex subsets A and B
   public int lengthSubset(Iterable<Integer> subsetA, Iterable<Integer> subsetB)

   // a shortest common ancestor of vertex subsets A and B
   public int ancestorSubset(Iterable<Integer> subsetA, Iterable<Integer> subsetB)

   // unit testing (required)
   public static void main(String[] args)

}

Corner cases.  Throw an IllegalArgumentException in the following situations:

• The argument to the constructor is not a rooted DAG
• Any argument is null
• Any vertex argument is outside its prescribed range
• Any iterable argument contains zero vertices
• Any iterable argument contains a null item

Basic performance requirements.  Your implementation must achieve the following worst-case performance requirements, where E and V are the number of edges and vertices in the digraph, respectively.

• Your data type must use \(O(E + V)\) space.
• All methods and the constructor must take \(O(E + V)\) time.

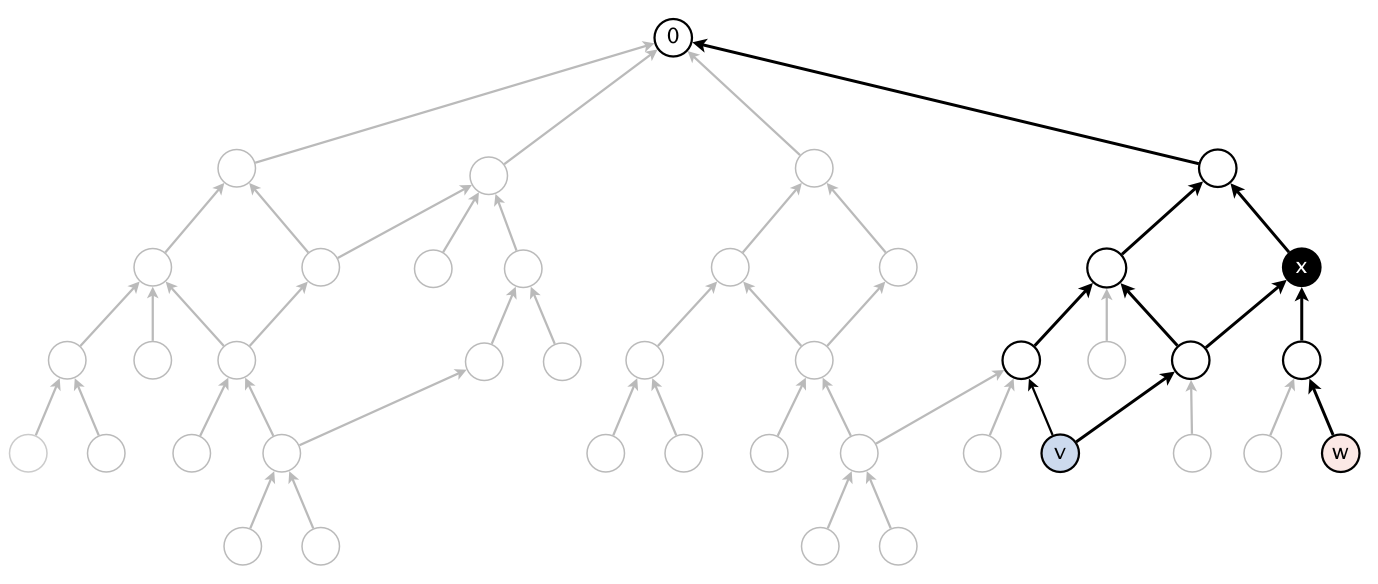
Additional performance requirements (for extra credit).  In addition, the methods length(), lengthSubset(), ancestor(), and ancestorSubset() must take time proportional to the number of vertices and edges reachable from the argument vertices (or better), For example, to compute the shortest common ancestor of v and w in the following digraph, your algorithm can examine only the highlighted vertices and edges; it cannot initialize any vertex-indexed arrays.

Unit testing.  In your main() method you will implement a test that creates a specific digraph for which you know the lengthSubset() of. Before describing the unit test, we will remind you of a definition.

A directed path of length \(\ell\) is a sequence of \(\ell\) directed edges that connect \(\ell + 1\) vertices. The starting vertex of a path is the vertex from which the path starts, i.e., the sole vertex with one outgoing and no incoming path edges. The ending vertex of a path is the vertex from which the path starts, i.e., the sole vertex with one incoming and no outgoing path edges. (All other vertices have one outgoing and one incoming edge each.)

The unit test you must implement is the following:

• Get two integers \(n\) and \(m\) as a command-line arguments and create two arrays of \(n\) integers each, pathsA and pathsB. Fill each array with uniform random integers between 1 and \(m\).
• The rooted DAG you shall create should be a graph given by the union of \(2n\) directed paths all with the same ending vertex, which is thus the root vertex (it might simplify your implementation to designate vertex 0 as the root vertex). The lengths of these paths shall be given by the values in pathsA and pathsB.
• Let \(S_A\) and \(S_B\) be the sums of pathsA and pathsB, respectively. Create a Digraph with \(S_A + S_B + 1\) vertices, whose edges form \(2n\) edge-disjoint paths with lengths given by pathsA and pathsB (see below for an example).
• Create a ShortestCommonAncestor object with this graph and run lengthSubset() with subsetA given by the starting vertices corresponding to the directed paths from pathsA, and subsetB given by the starting vertices corresponding to the directed paths from pathsB.
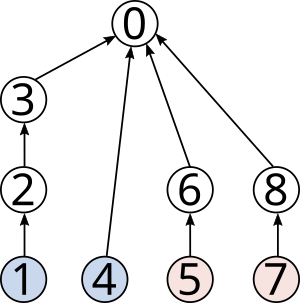
• Note that the expected result of the above lengthSubset() run should be exactly the sum of the minimum integer in pathsA and the minimum integer in pathsB. Thus, check that the output of lengthSubset() matches this sum and print a message (e.g. "Error!") if not.

As an example, suppose \(n = 2\), \(m = 3\), pathsA = {3, 1}, and pathsB = {2, 2}. Then the following image represents this instance, with the colored vertices representing the two subsets.

Note that the number of vertices and edges of this graph will be on the \(\Theta(nm)\), so a correct implementation should take no more than a few seconds when \(n\) and \(m\) are \(1,000\).

Testing. For additional testing, see the Checklist, in particular the section Input, Output, and Testing.

Measuring the semantic relatedness of two nouns. Semantic relatedness refers to the degree to which two concepts are related. Measuring semantic relatedness is a challenging problem. For example, you consider George W. Bush and John F. Kennedy (two U.S. presidents) to be more closely related than George W. Bush and chimpanzee (two primates). It might not be clear whether George W. Bush and Eric Arthur Blair are more related than two arbitrary people. However, both George W. Bush and Eric Arthur Blair (a.k.a. George Orwell) are famous communicators and, therefore, closely related.

We define the semantic relatedness of two WordNet nouns x and y as follows:

• A = set of synsets in which x appears

• B = set of synsets in which y appears

• distance(x, y) = length of shortest ancestral path of subsets A and B

• sca(x, y) = a shortest common ancestor of subsets A and B

This is the notion of distance that you will use to implement the distance() and sca() methods in the WordNet data type.

Outcast detection. Given a list of WordNet nouns x₁, x₂, ..., x_n, which noun is the least related to the others? To identify an outcast, compute the sum of the distances between each noun and every other one:

d_i   =   distance(x_i, x₁)   +   distance(x_i, x₂)   +   ...   +   distance(x_i, x_n)

Implement an immutable data type Outcast with the following API:

public class Outcast {

   // constructor takes a WordNet object
   public Outcast(WordNet wordnet)

   // given an array of WordNet nouns, return an outcast
   public String outcast(String[] nouns)

   // test client (see below)
   public static void main(String[] args)

}

Corner cases. Assume that the argument to outcast() contains only valid WordNet nouns and that it contains at least two such nouns.

Unit testing.  You don't need to create unit tests. Use the testing client and the examples in the Checklist to help you test your implementation.

Deliverables. Submit WordNet.java, ShortestCommonAncestor.java, and Outcast.java. Also submit any other supporting files (excluding those in algs4.jar). You may not call any library functions other than those in java.lang, java.util, and algs4.jar. Finally, submit readme.txt and acknowledgments.txt files and answer the questions.

Grading.

file	points
WordNet.java	12
ShortestCommonAncestor.java	16
Outcast.java	6
readme.txt	6
	40

Reminder: You can lose up to 4 points for breaking style principles and up to 3 points for not implementing the ShortestCommonAncestor unit tests.

Extra credit: You can earn 1–3 bonus points for meeting the additional performance requirements in ShortestCommonAncestor.