 Percolation
Percolation
Write a program to estimate the value of the percolation threshold via Monte Carlo simulation.
Install a Java programming environment. Install a Java programming environment on your computer. We recommend (but do not require) these step-by-step instructions for Mac OS X, Windows, or Linux.
If you followed our instructions, the commands javac-algs4 and java-algs4
will classpath in algs4.jar,
which contains Java classes for I/O and all of the algorithms in the textbook.
Percolation. Given a composite systems comprised of randomly distributed insulating and metallic materials: what fraction of the materials need to be metallic so that the composite system is an electrical conductor? Given a porous landscape with water on the surface (or oil below), under what conditions will the water be able to drain through to the bottom (or the oil to gush through to the surface)? Scientists have defined an abstract process known as percolation to model such situations.
The model. We model a percolation system using an n-by-n grid of sites. Each site is either open or blocked. A full site is an open site that can be connected to an open site in the top row via a chain of neighboring (left, right, up, down) open sites. We say the system percolates if there is a full site in the bottom row. In other words, a system percolates if we fill all open sites connected to the top row and that process fills some open site on the bottom row. (For the insulating/metallic materials example, the open sites correspond to metallic materials, so that a system that percolates has a metallic path from top to bottom, with full sites conducting. For the porous substance example, the open sites correspond to empty space through which water might flow, so that a system that percolates lets water fill open sites, flowing from top to bottom.)
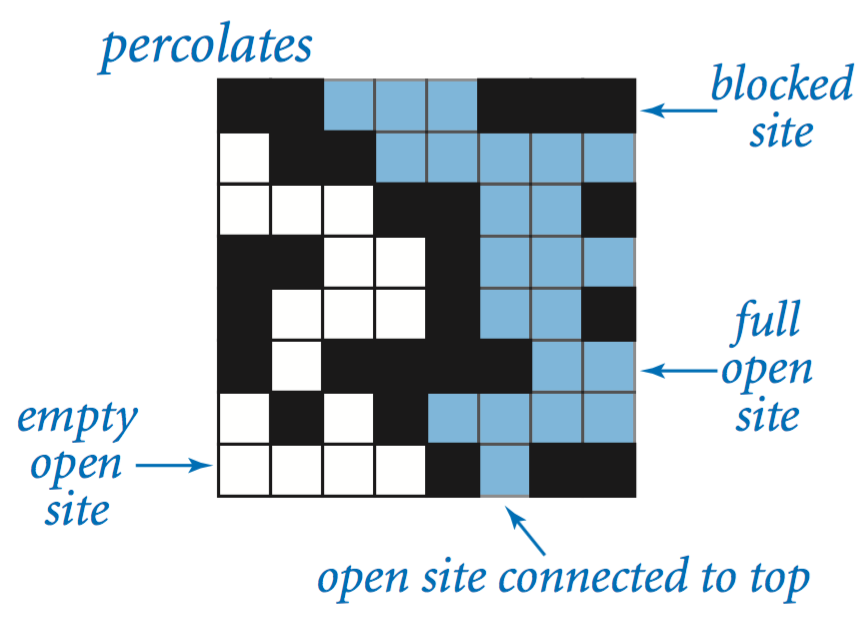
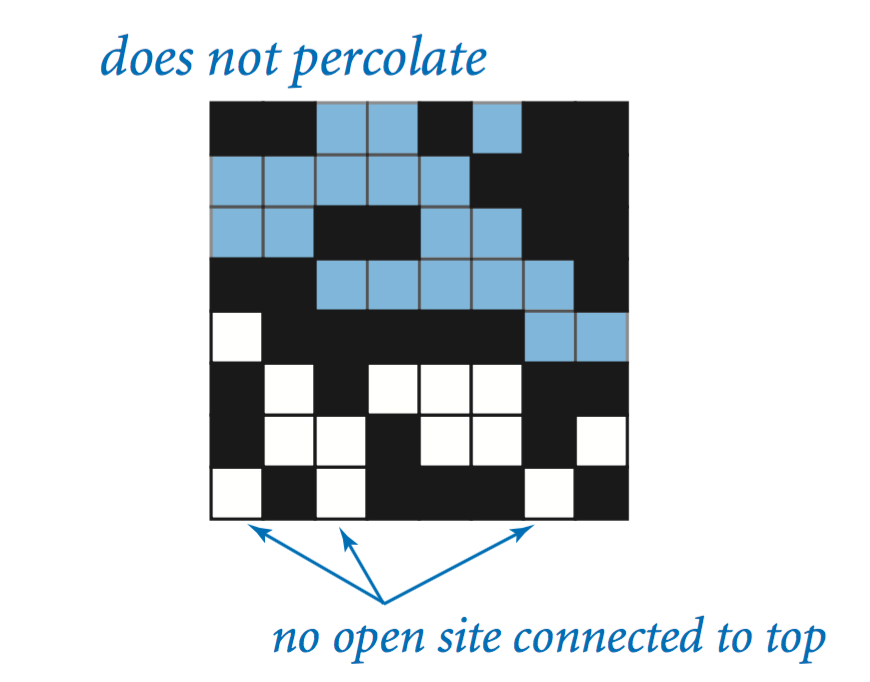
The problem. In a famous scientific problem, researchers are interested in the following question: if sites are independently set to be open with probability p (and, therefore, blocked with probability 1 − p), what is the probability that the system percolates? When p equals 0, the system does not percolate; when p equals 1, the system percolates. The plots below show the site vacancy probability p versus the percolation probability for random 20-by-20 grids (left) and 100-by-100 grids (right).
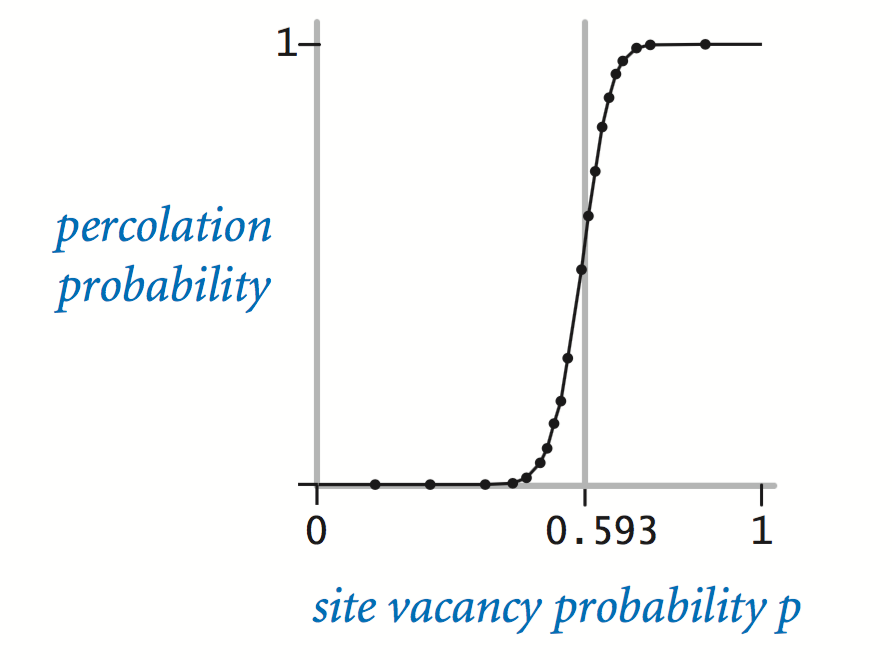
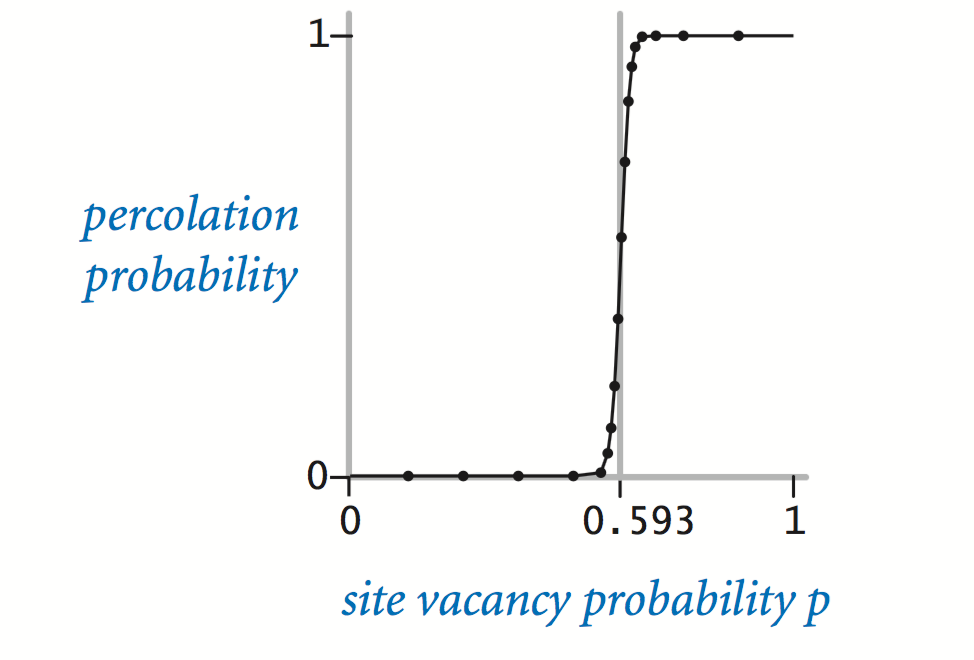
When n is sufficiently large, there is a threshold value p* such that when p < p* a random n-by-n grid almost never percolates, and when p > p*, a random n-by-n grid almost always percolates. No mathematical solution for determining the percolation threshold p* has yet been derived. Your task is to write a computer program to estimate p*.
Percolation data type.
To model a percolation system, create a data type Percolation with the following API:
public class Percolation {
// creates n-by-n grid, with all sites initially blocked
public Percolation(int n)
// opens the site (row, col) if it is not open already
public void open(int row, int col)
// is the site (row, col) open?
public boolean isOpen(int row, int col)
// is the site (row, col) full?
public boolean isFull(int row, int col)
// returns the number of open sites
public int numberOfOpenSites()
// does the system percolate?
public boolean percolates()
// unit testing (required)
public static void main(String[] args)
}
Corner cases. By convention, the row and column indices are integers between 0 and n − 1, where (0, 0) is the upper-left site.
IllegalArgumentException
if any argument to open(), isOpen(), or isFull()
is outside its prescribed range.
IllegalArgumentException in the constructor if n ≤ 0.
Unit testing.
Your main() method must call each public constructor and method directly and
help verify that they work as prescribed (e.g., by printing results to standard output).
Performance requirements.
The constructor must take \(\Theta(n^2)\) time;
all instance methods must take
\(\Theta(1)\) time plus \(\Theta(1)\) calls to
union() and find().
Monte Carlo simulation. To estimate the percolation threshold, consider the following computational experiment:
For example, if sites are opened in a 20-by-20 grid according to the snapshots below, then our estimate of the percolation threshold is 204/400 = 0.51 because the system percolates when the 204th site is opened.

| 
| 
| 
|
By repeating this computation experiment T times and averaging the results, we obtain a more accurate estimate of the percolation threshold. Let xt be the fraction of open sites in computational experiment t. The sample mean \(\overline x\) provides an estimate of the percolation threshold; the sample standard deviation s measures the sharpness of the threshold.
\[ \overline x = \frac{x_1 \, + \, x_2 \, + \, \cdots \, + \, x_{T}}{T}, \quad s^2 = \frac{(x_1 - \overline x )^2 \, + \, (x_2 - \overline x )^2 \,+\, \cdots \,+\, (x_{T} - \overline x )^2}{T-1} \]Assuming T is sufficiently large (say, at least 30), the following provides a 95% confidence interval for the percolation threshold:
\[ \left [ \overline x - \frac {1.96 s}{\sqrt{T}}, \;\; \overline x + \frac {1.96 s}{\sqrt{T}} \right] \]
To perform a series of computational experiments, create a data type PercolationStats
with the following API:
public class PercolationStats {
// perform independent trials on an n-by-n grid
public PercolationStats(int n, int trials)
// sample mean of percolation threshold
public double mean()
// sample standard deviation of percolation threshold
public double stddev()
// low endpoint of 95% confidence interval
public double confidenceLow()
// high endpoint of 95% confidence interval
public double confidenceHigh()
// test client (see below)
public static void main(String[] args)
}
The constructor takes two arguments n and T, and perform T independent computational experiments (discussed above) on an n-by-n grid. Using this experimental data, it calculates the mean, standard deviation, and the 95% confidence interval for the percolation threshold.
Standard libraries.
Use
StdRandom
to generate random numbers; use
StdStats
to compute the sample mean and standard deviation;
use Stopwatch
to measure the running time.
Corner cases.
Throw an IllegalArgumentException in the constructor
if either n ≤ 0 or T ≤ 0.
Test client. The test client takes two command-line arguments n and T and prints the relevant statistics for T computational experiments on an n-by-n grid.
~/Desktop/percolation> java-algs4 PercolationStats 200 100 mean() = 0.592993 stddev() = 0.008770 confidenceLow() = 0.591275 confidenceHigh() = 0.594712 elapsed time = 0.373 ~/Desktop/percolation> java-algs4 PercolationStats 200 100 mean() = 0.592877 stddev() = 0.009991 confidenceLow() = 0.590919 confidenceHigh() = 0.594835 elapsed time = 0.364 ~/Desktop/percolation> java-algs4 PercolationStats 2 100000 mean() = 0.666948 stddev() = 0.117752 confidenceLow() = 0.666218 confidenceHigh() = 0.667677 elapsed time = 0.087
Comparison of two data structures.
Implement Percolation using the quick-find algorithm, then
using the weighted quick-union algorithm. Compare the performance of the two algorithms.
Percolation using
QuickFindUF.
What is the largest values of n that
PercolationStats can handle in less than one minute on your computer when
performing T = 100 trials?
Percolation using
WeightedQuickUnionUF.
What is the largest values of n that
PercolationStats can handle in less than one minute on your computer when
performing T = 100 trials?
Project files. The file percolation.zip contains a test client and sample input files.
Submission.
Submit only Percolation.java (using the weighted quick-union algorithm
from
WeightedQuickUnionUF)
and PercolationStats.java.
We will supply algs4.jar.
Do not call any library functions except those in
StdIn,
StdOut,
StdRandom,
StdStats,
Stopwatch,
WeightedQuickUnionUF,
and
java.lang.
Finally, submit readme.txt
and acknowledgments.txt
files and answer the questions.
Grading.
file points Percolation.java22 PercolationStats.java12 readme.txt6 40
Reminder: You can lose up to 4 points for poor style and up to 4 points for inadequate unit testing.
Extra credit: You can earn 1 point of extra credit for
handling backwash in a time-efficient manner,
and 2 additional points of extra credit for doing so using only
\(\sim n^2\) additional memory beyond that of the base solution.