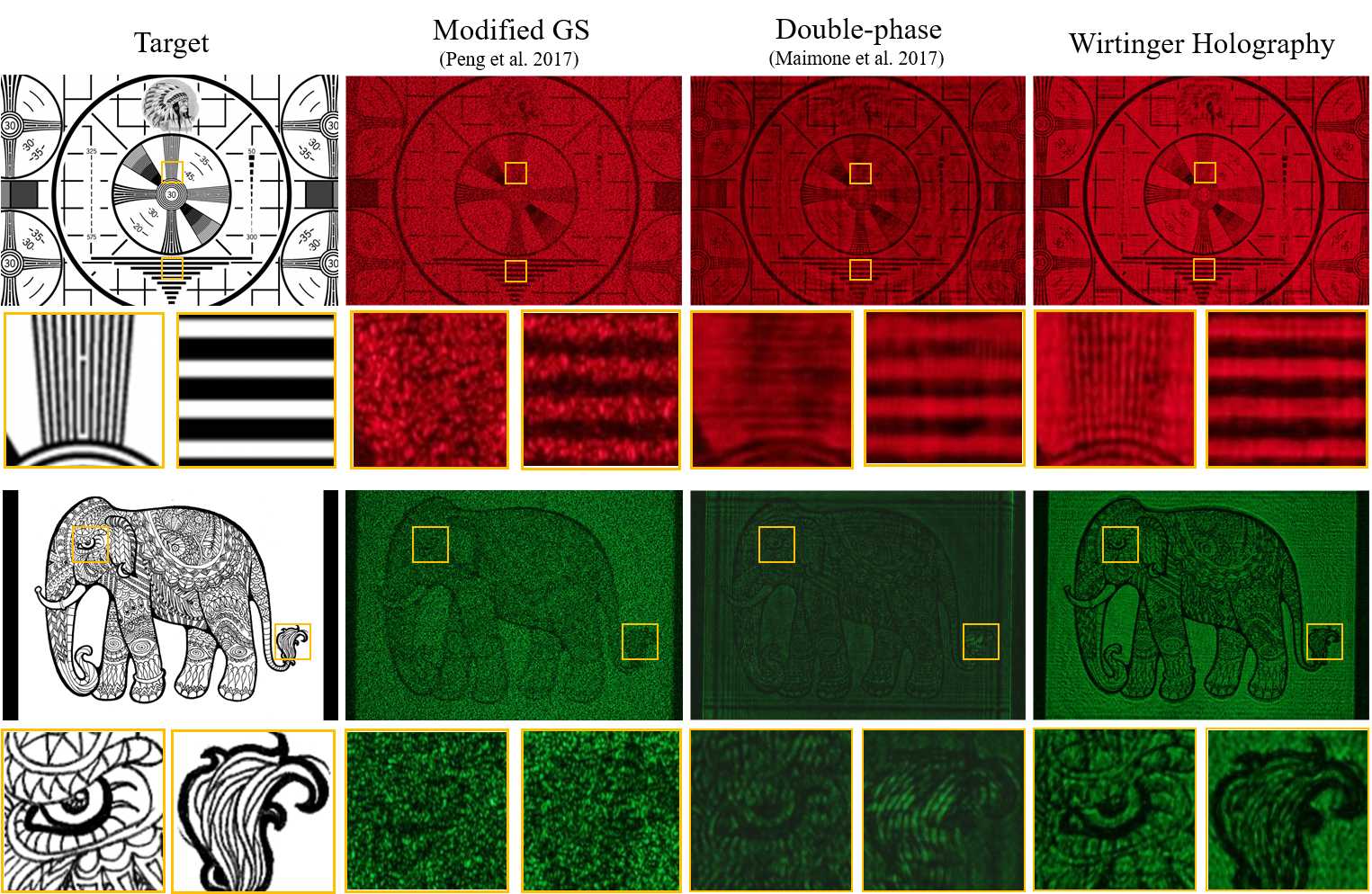
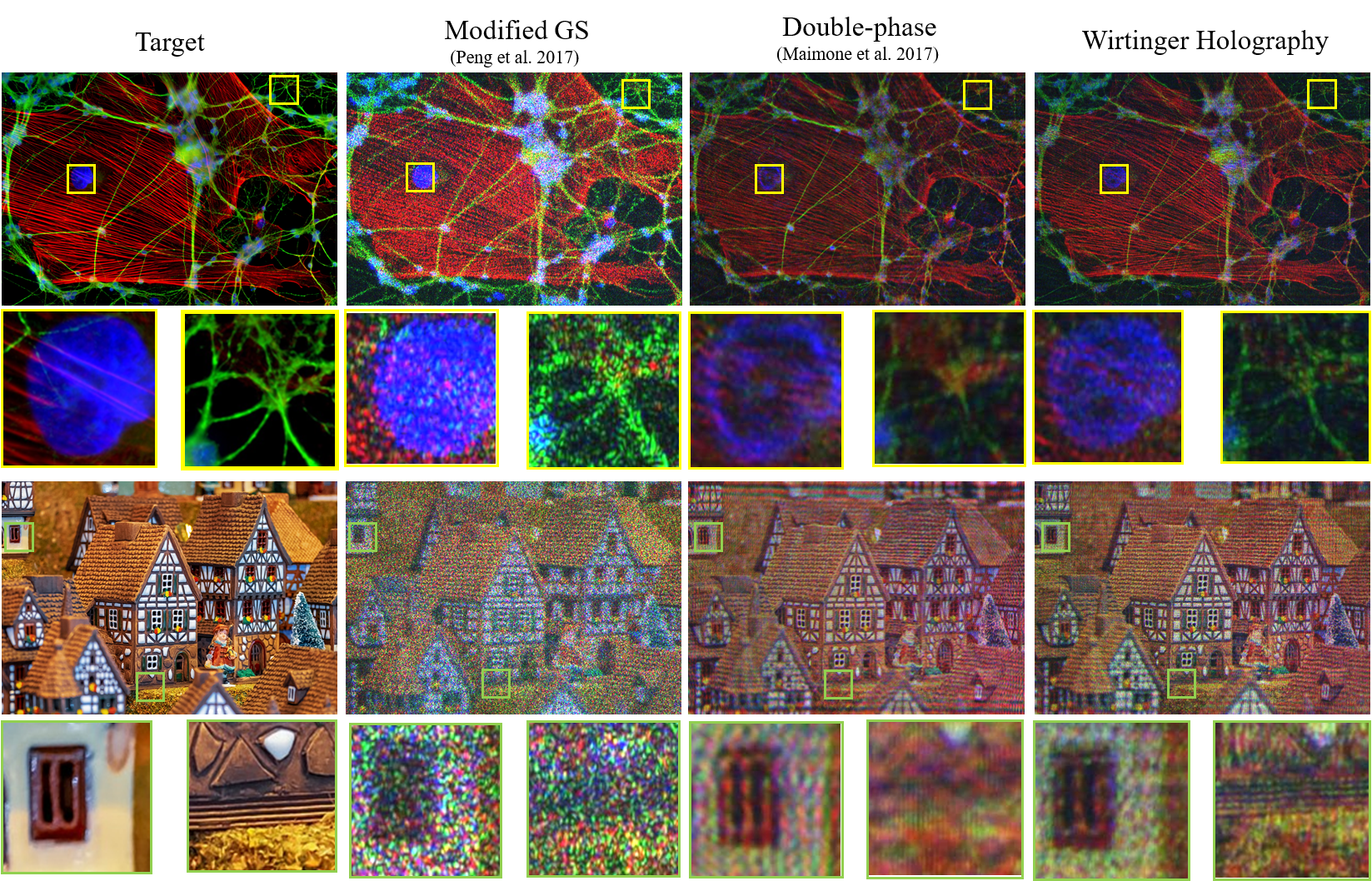
Wirtinger Holography on a Display Prototype. To compute phase-only modulation patterns, we depart from existing iterative projection algorithms,
such as error-reduction Gerchberg-Saxton methods [Gerchberg 1972; Peng et al. 2017], and heuristic encoding approximations, such as the double phase
encoding method [Hsueh and Sawchuk 1978]. Instead, we revisit the use of formal optimization using complex Wirtinger derivatives for the underlying
phase retrieval problem. We built a near-eye display prototype using a phase-only spatial light modulator (SLM) and off-the-shelf optics (left). Compared to
holographic reconstructions at a set focal distance from the existing methods [Peng et al. 2017] (center left) and [Maimone et al. 2017] (center right), the
proposed Wirtinger holography substantially reduces reconstruction artefacts on our prototype, while achieving an order of magnitude reduced error in
simulation. Mouse embryo image by Miltenyi Biotec.
|
Near-eye displays using holographic projection are emerging as an exciting display approach for virtual and augmented reality at high-resolution
without complex optical setups —
shifting optical complexity to computation. While precise phase modulation hardware is becoming available, phase
retrieval algorithms are still in their infancy, and holographic display approaches resort to heuristic encoding methods or iterative methods relying
on various relaxations.
In this work, we depart from such existing approximations and solve the
phase retrieval problem for a hologram of a scene at a single depth at a given
time by revisiting complex Wirtinger derivatives, also extending our framework to render 3D volumetric scenes. Using Wirtinger derivatives allows
us to pose the phase retrieval problem as a quadratic problem which can be
minimized with first-order optimization methods. The proposed Wirtinger Holography is flexible and facilitates the use of different loss functions, including learned perceptual losses parametrized by deep neural networks,
as well as stochastic optimization methods. We validate this framework
by demonstrating holographic reconstructions with an order of magnitude
lower error, both in simulation and on an experimental hardware prototype..
|