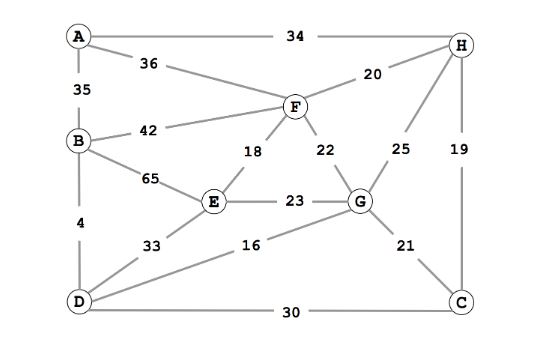
Give the list of edges in the MST in the order that Kruskal's algorithm includes them.
Give the list of edges in the MST in the order that Prim's algorithm includes them. Start Prim's algorithm from vertex A. Answers
Give the list of edges in the MST in the order that Kruskal's algorithm includes them.
Give the list of edges in the MST in the order that Prim's algorithm includes them. Start Prim's algorithm from vertex F. Answers
Give the list of edges in the MST in the order that Kruskal's algorithm includes them.
Give the list of edges in the MST in the order that Prim's algorithm includes them. Start Prim's algorithm from vertex A. Answers