
Computer Science 226
Algorithms and Data Structures
Spring 2013
|
|
|
Course Information |
Assignments |
Exercises |
Lectures |
Exams |
Precepts |
Booksite
Max Flow
Things to Know Before Lecture
- Know the basic concepts and definitions (see checkpoint below for a concise visual representation of these definitions).
- Definition of a flow network and of edge capacity. (pg 888)
- Definition of an st flow (an assignment of value to every edge) (pg 888).
- Definition of influx and outflux of a vertex (pg 888).
- Definition of the value of an st flow: Influx at the sink vertex.
- Definition of an st cut (and how to determine its capacity) (pg 892).
- Definition of a max st flow (pg 888).
- Definition of a min st cut (pg 893).
- Definition of an augmenting path (pg 891).
- Understand the steps of the Ford-Fulkerson algorithm (you do not need to know how to find an augmenting path efficiently).
- Understand why the following questions about Ford-Fulkerson are interesting (answers to be addressed in lecture). You do not need to understand how to solve these problems before lecture.
- How do we find an augmenting path?
- If Ford-Fulkerson terminates, does it always compute a maxflow?
- Does Ford-Fulkerson always terminate? If so, how after how many augmentations?
- How do we compute a mincut?
It's not absolutely necessary to be able to solve a Ford-Fulkerson problem by hand, but it's probably a good idea. See checklist problem #2.
Pre-Lecture Preparation Guide.
High priority videos are in red. Low priority videos are in blue.
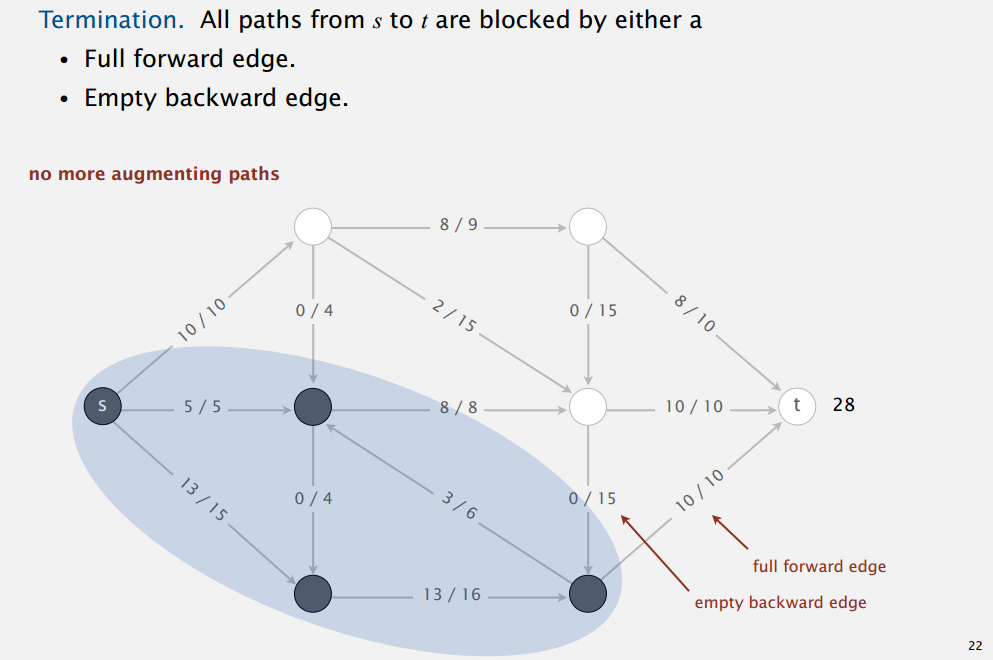
Checkpoint 1: Everything in the diagram below should make sense. Specifically, you should understand:
- That the first number on each edge is the "edge flow", and the second number is the "edge capacity".
- That the vertices in blue are on the s side of the s-t cut, and the vertices in white are on the t side.
- That s is the source, and t is the sink.
- That the value of this flow is 28.
- That the capacity of the min-cut is 28.
- That there are no more augmenting paths, because all the forward edges from s-t to are full, and all the backward edges from t-s are empty.
Checkpoint 2: Optional: You should be able to solve a max flow exercise using Ford-Fulkerson. We will be going through the demo in the slides, though, so if you don't get around to it, no big deal. Recommended technique: Try to do the problem in the demo, then come back and see if your answer was right. You do NOT need to identify the same sequence of augmenting paths (unlike Prim's / Kruskal's / Dijkstra's, there is no canonical order!).
