Re-affirm the atomic nature of matter by tracking the motion of particles undergoing Brownian motion, fitting this data to Einstein's model, and estimating Avogadro's number.
Historical perspective. The atom played a central role in 20th century physics and chemistry, but prior to 1908 the reality of atoms and molecules was not universally accepted. In 1827, the botanist Robert Brown observed the random erratic motion of wildflower pollen grains immersed in water using a microscope. This motion would later become known as Brownian motion. Einstein hypothesized that this Brownian motion was the result of millions of tiny water molecules colliding with the larger pollen grain particles.
In one of his "miraculous year" (1905) papers, Einstein formulated a quantitative theory of Brownian motion in an attempt to justify the "existence of atoms of definite finite size." His theory provided experimentalists with a method to count molecules with an ordinary microscope by observing their collective effect on a larger immersed particle. In 1908 Jean Baptiste Perrin used the recently invented ultramicroscope to experimentally validate Einstein's kinetic theory of Brownian motion, thereby providing the first direct evidence supporting the atomic nature of matter. His experiment also provided one of the earliest estimates of Avogadro's number. For this work, Perrin won the 1926 Nobel Prize in physics.
The problem. In this assignment, you will redo a version of Perrin's experiment. Your job is greatly simplified because with modern video and computer technology (in conjunction with your programming skills), it is possible to accurately measure and track the motion of an immersed particle undergoing Brownian motion. We supply video microscopy data of polystyrene spheres ("beads") suspended in water, undergoing Brownian motion. Your task is to write a program to analyze this data, determine how much each bead moves between observations, fit this data to Einstein's model, and estimate Avogadro's number.
The data. We provide ten datasets, obtained by William Ryu using fluorescent imaging. Each run contains a sequence of two hundred 640-by-480 color JPEG images, frame00000.jpg through frame00199.jpg and is stored in a subdirectory run_1 through run_10.
Here is a movie [ avi · mov ] of several beads undergoing Brownian motion. Below is a typical raw image (left) and a cleaned up version (right) using thresholding, as described below.
Each image shows a two-dimensional cross section of a microscope slide. The beads move in and out of the microscope's field of view (the x- and y-directions). Beads also move in the z-direction, so they can move in and out of the microscope's depth of focus; this results in halos, and it can also result in beads completely disappearing from the image.
Particle identification. The first challenge is to identify the beads amidst the noisy data. Each image is 640-by-480 pixels, and each pixel is represented by a Color object which needs to be converted to a luminance value ranging from 0.0 (black) to 255.0 (white). Whiter pixels correspond to beads (foreground) and blacker pixels to water (background). We break the problem into three pieces: (i) read in the picture, (ii) classify the pixels as foreground or background, and (iii) find the disc-shaped clumps of foreground pixels that constitute each bead.
Create a helper data type Blob that has the following API.
public class Blob
------------------------------------------------------------------------------------------------
public Blob() // construct an empty blob
public void add(int i, int j) // add a pixel (i, j) to the blob
public int mass() // return number of pixels added = its mass
public double distanceTo(Blob b) // return distance between centers of masses of this blob and b
public String toString() // return string containing this blob's mass and center of mass
// format center-of-mass coordinates with 4 digits to right
// of decimal point
Next, write a data type BlobFinder that has the following API. Use depth-first search to efficiently identify the blobs.
Write a main() method in BlobFinder.java that takes an integer P, a double value tau, and the name of a JPEG file as command-line arguments. It then creates a BlobFinder object using a luminance threshold of tau. Next, it prints out all of the beads with at least P pixels; finally, it prints out all of the blobs (beads with at least 1 pixel).public class BlobFinder ------------------------------------------------------------------------------------------------ // find all blobs in the picture using the luminance threshold tau public BlobFinder(Picture picture, double tau) // return the number of beads with >= P pixels public int countBeads(int P) // return all beads with >= P pixels public Blob[] getBeads(int P)
The program identifies 15 blobs in the sample frame, 13 of which are beads. Our string representation of a blob specifies its mass (number of pixels) and its center of mass (in the 640-by-480 picture). By convention, pixels are measured from left-to-right, and from top-to-bottom (instead of bottom-to-top).% java BlobFinder 25 180.0 run_1/frame00001.jpg 13 Beads: 29 (214.7241, 82.8276) 36 (223.6111, 116.6667) 42 (260.2381, 234.8571) 35 (266.0286, 315.7143) 31 (286.5806, 355.4516) 37 (299.0541, 399.1351) 35 (310.5143, 214.6000) 31 (370.9355, 365.4194) 28 (393.5000, 144.2143) 27 (431.2593, 380.4074) 36 (477.8611, 49.3889) 38 (521.7105, 445.8421) 35 (588.5714, 402.1143) 15 Blobs: 29 (214.7241, 82.8276) 36 (223.6111, 116.6667) 1 (254.0000, 223.0000) 42 (260.2381, 234.8571) 35 (266.0286, 315.7143) 31 (286.5806, 355.4516) 37 (299.0541, 399.1351) 35 (310.5143, 214.6000) 31 (370.9355, 365.4194) 28 (393.5000, 144.2143) 27 (431.2593, 380.4074) 36 (477.8611, 49.3889) 38 (521.7105, 445.8421) 35 (588.5714, 402.1143) 13 (638.1538, 155.0000)
Particle tracking. The next step is to determine how far a bead moved from one time step t to the next t + Δt. For our data, Δ t = 0.5 seconds per frame. We assume the data is such that each bead moves a relatively small amount, and that two beads do not collide. (However, we must account for the possibility that the bead disappears from the frame, either by departing the microscope's field of view in the x- or y- direction, or moving out of the microscope's depth of focus in the z-direction.) Thus, for each bead at time t + Δt, we calculate the closest bead at time t (in Euclidean distance) and identify these two as the same beads. However, if the distance is too large (greater than delta pixels) we assume that one of the beads has either just begun or ended its journey. We record the displacement that each bead travels in the Δt units of time.
Write a main() method in BeadTracker.java that takes an integer P, a double value tau, a double value delta, and a sequence of JPEG filenames as command-line arguments, identifies the beads (using the specified values of P and tau) in each JPEG image (using BlobFinder), and prints out (one per line, formatted with 4 decimal places to the right of decimal point) the radial displacement that each bead moves from one frame to the next (assuming it is no more than delta). Note that it is not necessary to explicitly track a bead through a sequence of frames—you only need to worry about identifying the same bead in two consecutive frames.
% java BeadTracker 25 180.0 25.0 run_1/*.jpg 7.1833 4.7932 2.1693 5.5287 5.4292 4.3962 ...
Data analysis. Einstein's theory of Brownian motion connects microscopic properties (e.g., radius, diffusivity) of the beads to macroscopic properties (e.g., temperature, viscosity) of the fluid in which the beads are immersed. This amazing theory enables us to estimate Avogadro's number with an ordinary microscope by observing the collective effect of millions of water molecules on the beads.
For our data, Δt = 0.5 so our estimate for σ2 is an estimate for D as well. The radial displacements ri are measured in pixels: to convert to meters, multiply by 0.175 * 10-6 (meters per pixel).
= viscosity of water = 9.135 * 10-4
N*s/m2
(at room temperature)
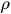= radius of bead = 0.5 * 10-6 meters
and k is the Boltzmann constant. All parameters are given in SI units. The Boltzmann constant is a fundamental physical constant that relates the average kinetic energy of a molecule to its temperature. We estimate k by measuring all of the parameters in the Stokes-Einstein equation, and solving for k.
For the final part, write a main() method in Avogadro.java that reads in the displacements from standard input and computes an estimate of Boltzmann's constant and Avogadro's number using the formulas described above.
% more displacements-run_1.txt % java BeadTracker 25 180.0 25.0 run_1/*.jpg | java Avogadro 7.1833 Boltzmann = 1.2535e-23 4.7932 Avogadro = 6.6330e+23 2.1693 5.5287 5.4292 4.3962 ... % java Avogadro < displacements-run_1.txt Boltzmann = 1.2535e-23 Avogadro = 6.6330e+23
Output formats. Use four digits to the right of the decimal place for all of your floating point outputs whether they are in floating point format or exponential format.
Running time analysis. Formulate a hypothesis for the running time (in seconds) of BeadTracker as a function of the input size N (total number of pixels read in across all frames being processed). Justify your hypothesis in your readme.txt file with empirical data.
Provided files. You can download the datasets and other files mentioned above as a 67.1 MB zip file. (You can alternatively use the course FTP site.)
Submission. Submit Blob.java, BlobFinder.java, BeadTracker.java and Avogadro.java. Finally, submit a readme.txt file (or partner readme file) and answer the questions including the running time analysis. If your program has any dependencies other than the standard libraries and Luminance.java, submit them as well.