| NAME AND DESCRIPTION |
N = 1 |
N = 2 |
N = 3 |
N = 4 |
N = 5 |
N = 6 |
Yannis Guzman
My creation was the Sierpinski Curve. It starts with a horizontal line; at each level of recursion, every line is replaced with a baseless trapezoid in a particular direction. As the level of recursion goes to infinity, it forms the Sierpinski Triangle. Challenges in writing it included line deletion (I ended up drawing over them with a larger PenRadius) and determining a way to generate the trapezoid points using only the line endpoints as input (seeing Euclid's method for drawing hexagons with circles on Wikipedia was chief inspiration). |
 |
 |
 |
 |
 |
 |
Cathy Chen
I referenced the book site first to have an idea of what kinds of designs I wanted to do. I first decided on doing a snowflake, which is why the design still looks like a snowflake a little. I spent a lot of time calculating out the special ratios and angles of all the hexagons, and how I wanted each successive level to fit into the next. I decided to shift the center of the main hexagon to the corner. I thought it looked a little like a web, so I added the additional lines and stuck a picture of a pig in the back, in honor of one of my favorite children's books, "Charlotte's Web." |
 |
 |
 |
 |
 |
 |
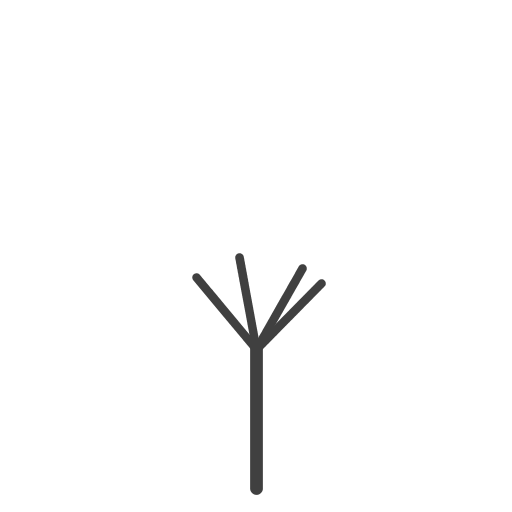
Laura Blue
I've drawn a cherry-blossom tree. My program adds a method to draw blossoms at the end of all branches -- but it only calls this method when the tree has many little branches so that we can consider the tree to be "budding." |
 |
 |
 |
 |
 |
 |
Brian Tu
For my creation, I drew a variant of the Koch quadratic type 2 curve. My algorithm works regardless what the start and end points are. Although it cannot be seen here, I modified the original Koch curve algorithm so that the image looks like it is traced out from start to finish, rather than recursively drawn. I did this by only having the last level of recursion actually draw anything. Although each unit in the drawing is actually not connected to the other ones, at greater N the final drawing looks more and more like one big line. Finally, I randomized the colors of each unit, making it look cooler. |
 |
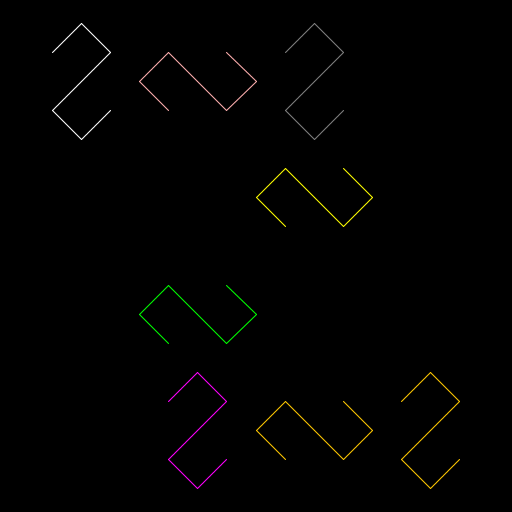 |
 |
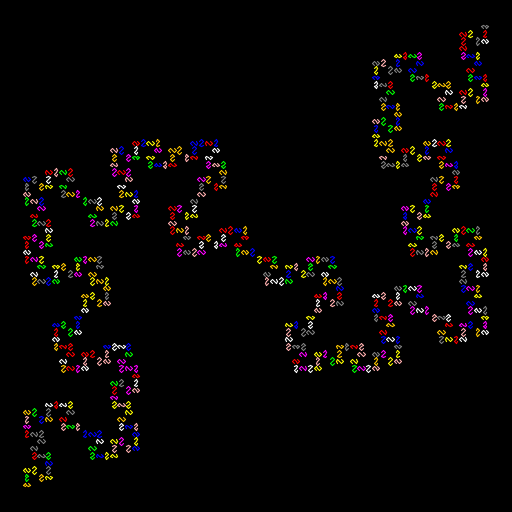 |
 |
 |
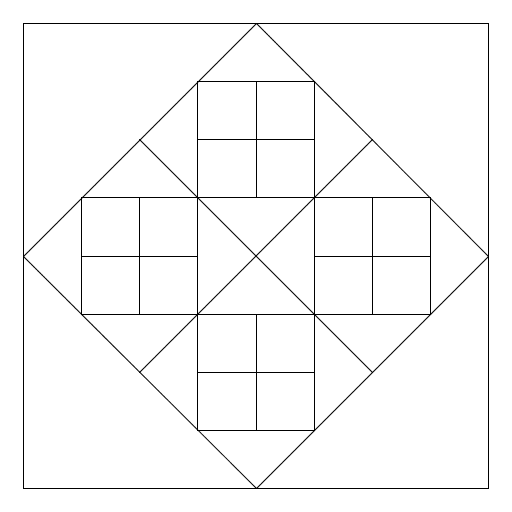
Christina Efthimion
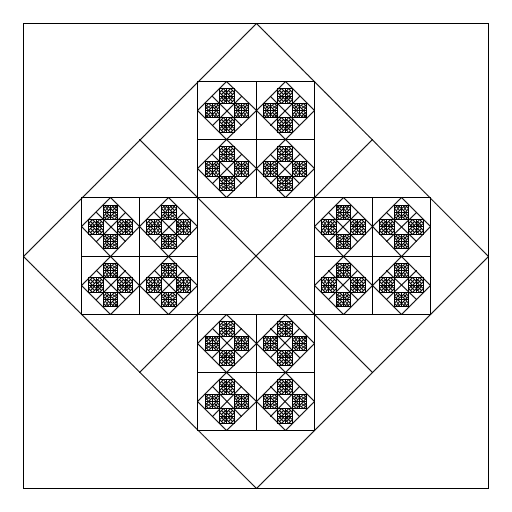
My artistic creation involves 4 squares inside a square but each square is tilted so the corners are on the midpoints of the larger squares. This involves two different drawing functions and two different recursion functions so that the tilted squares and traditional squares alternate. I started by using the program Htree as a model but I had to change it drastically to create my design. |
 |
 |
 |
 |
 |
 |
Colleen McCullough
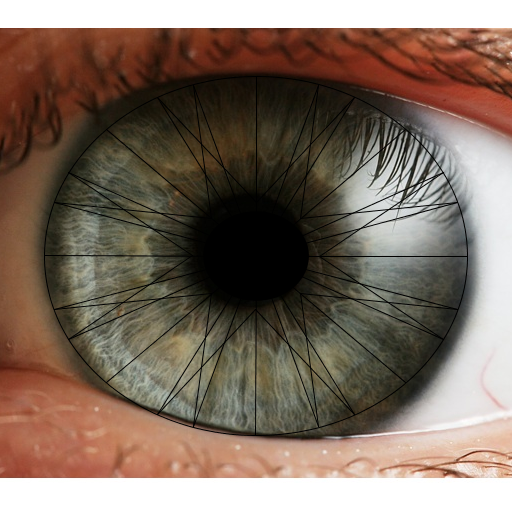
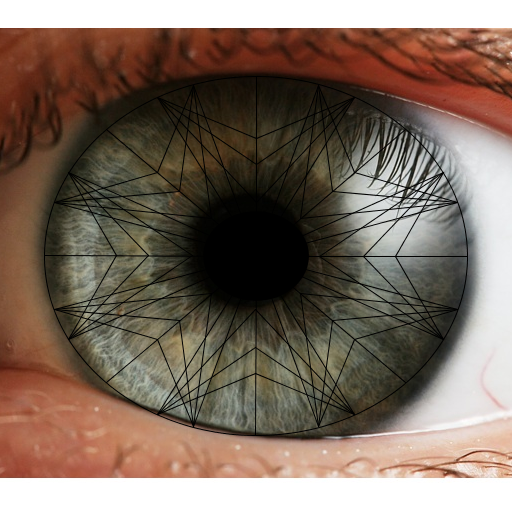
My art project is an eye with a design that represents the spokes of the iris. I based my program on Sierpinski, and didn't use any other sources. |
 |
 |
 |
 |
 |
 |
David Harris
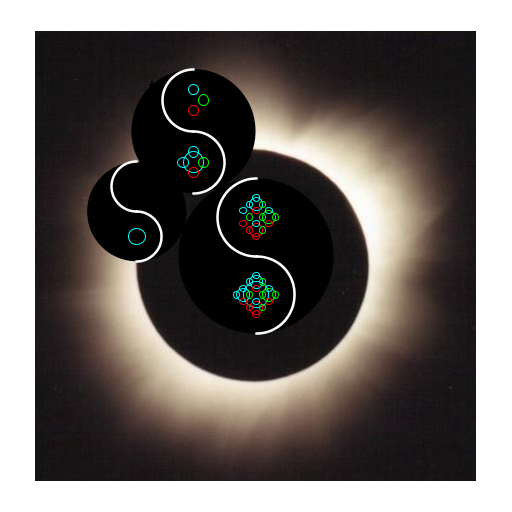
My artistic creation draws a spiral of Yin-Yang Symbols slowly decreasing in size while a recursive circle function inside the symbol slowly undoes its recursiveness. I call it "Chaos Control". |
 |
 |
 |
 |
 |
 |
Tharald Sund Fongaard
In my artistic creation i first wanted to make a flower inspired by the super popular computer game Minecraft (java). I wanted to make an inner bud and flower that was more freely spaced. I therefore chose to make recursive patterns on top each other. One of them is inspired by the function for drawing a "diamond" (page 142 in the book) and the other one I made myself with squares on squares. I also added a random color creator so that every square has a random color. (to make it artsy ofc) |
 |
 |
 |
 |
 |
 |
Hannah Sosebee
I really like fractals - the Koch curve is one that I draw often when I'm doodling, so it seemed like fun to create. Then I switched the colors, and made the size of the line and inverse function of the number of recursions, to make it look more interesting. |
 |
 |
 |
 |
 |
 |
Jessica Luo
I used a recursive function to draw two parabolic lines within a square. The parabolic lines formed the shape of an eye. Inside the eye, I drew two more squares with parabolic lines within them. I connected the two squares with parabolic lines. |
 |
 |
 |
 |
 |
 |
Katherine Flanigan
My program uses recursion to draw the pattern and layering of a peacock's feathers and adds the body (beak, eyes, and feet). I used trig to create the design of the feathers and to figure out how to adjust my code so that the true overall shape of the peacock's feathers maintained a particular shape once I began the overlapping to create the layers of feathers, while staying in proportion to the peacock's original body size. The higher the recursion, N, the more dense the layering of the feathers. |
 |
 |
 |
 |
 |
 |
Michelle Kiyeon Kim
My Art project creates a dandelion seed flying in the air, with input argument N rods of seeds attached to it. The most tricky part of the project was to place the rods in different angles, using math.cos and math.sin functions. I got the background image from http://www.portwallpaper.com/image/26471-dandelion.html, and drew the picture in white pencolor to make it seem more like a floating seed. |
 |
 |
 |
 |
 |
 |
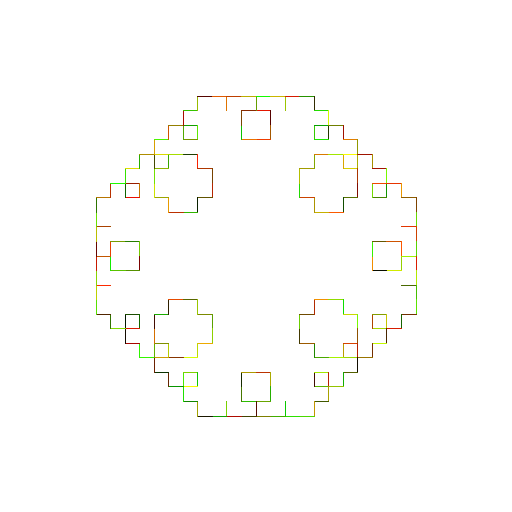
Ming-Ming Tran
It is a Levy's Tapestry - Levy's Curve executed on a box. I looked at each line segment individually to decide how to find the new point and angle of the line segment. I used http://mathworld.wolfram.com/LevyTapestry.html and http://library.thinkquest.org/26242/full/fm/fm19.html to help me visualize it. |
 |
 |
 |
 |
 |
 |
Matthew McDonald
My artistic compilation uses two recursions to draw two spiraling triangles on top of each other that are then filled in with random colors. The spirals are created by drawing triangles between weighted midpoints of the triangle they are inside. The amount of weight of each midpoint depends on how many iterations are requested. The colors are made via Math.random. |
 |
 |
 |
 |
 |
 |
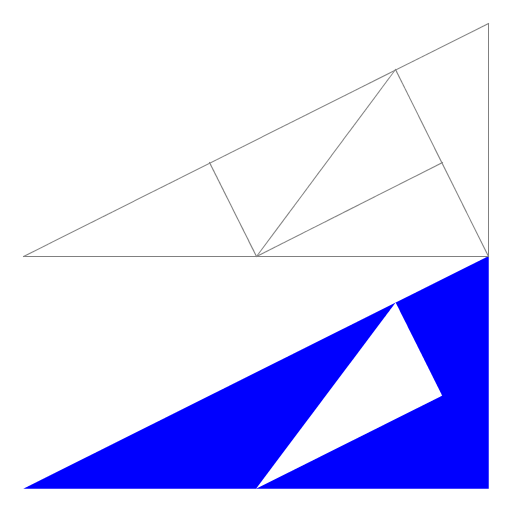
Matan Appelbaum
My program draws the Pinwheel fractal, discovered by John Conway. It is formed by cutting up a right triangle with legs 1 and 2 into 5 smaller copies of itself. The construction is shown above the fractal. The smaller triangles are rotated in such a way that the triangles in the fractal are rotated through infinitely many angles. This fractal is based on the example from http://en.wikipedia.org/wiki/Pinwheel_tiling. |
 |
 |
 |
 |
 |
 |
Nicholas Robinson
I took my inspiration from the book's vague description of how make a plasma cloud. The program repeatedly averages colors at the corners of the square and assigns this color, offset slightly, as a center color to determine the colors of the corners of smaller squares inside. At the base case, it draws these squares based on an average of the corners. |
 |
 |
 |
 |
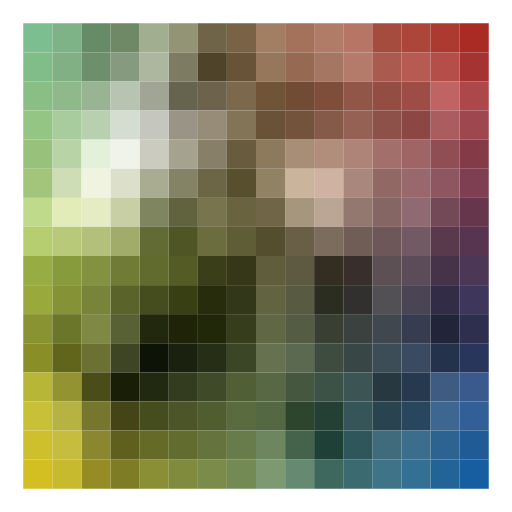 |
 |
Nicholas Horbelt
My artistic creation is a plant formed by a multitude of line segments of various lengths and angles. It was adapted from an L-system, or Lindenmayer system, plant fractal. |
 |
 |
 |
 |
 |
 |
Pui Yan Jane Leong
The idea of creating many funkybinnies first came from my idea of drawing disco bunnies, however, I could not find a nice disco background so I tried to put the bunnies against a pieceful grass background that I already had on my computer and it looked very nice so I changed my idea to peaceful funkybunnies insted. I changed the order of function calls so that the big bunny is drawn in frontof the small bunnies. |
 |
 |
 |
 |
 |
 |
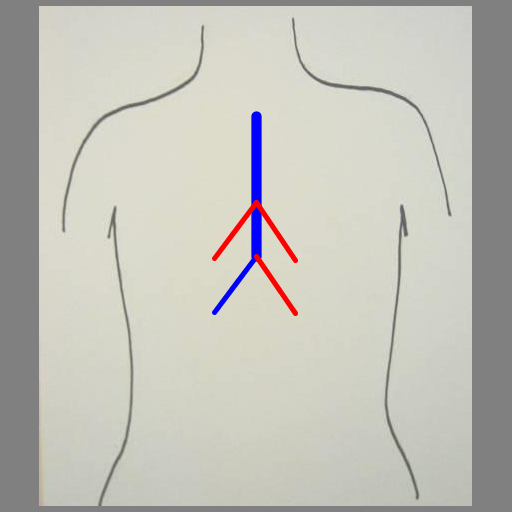
Paul Marano
This program was inspired by the images of trees and branches we mentioned in class and that one student created in the fall of 2010 (shown on the assignment page). It creates lungs in the same way a tree might be created, by recursively drawing a line segment with branching points. The output is a series of blood vessicles, randomly colored blue or red, branching off from one another at a random angle within a specified range to give the appearance of lungs. The branching points occur at the end of the vessicle and along it (at the golden ratio). |
 |
 |
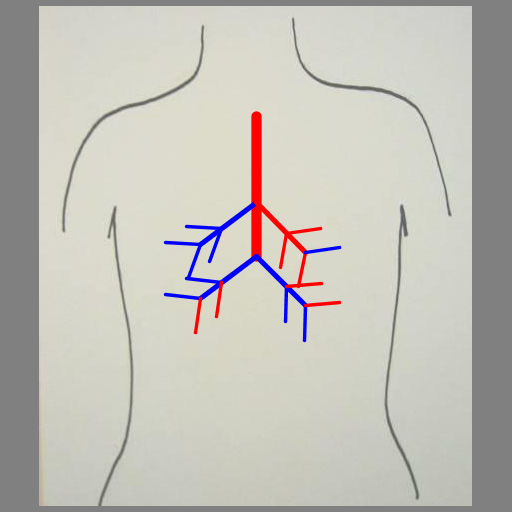 |
 |
 |
 |
Tiffany Cheezem
I made a fractal out of nine circles inscribed within a larger circle. |
 |
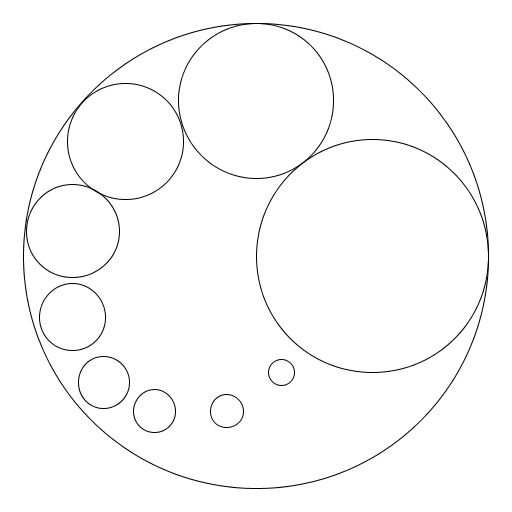 |
 |
 |
 |
 |
Alina Spiegel
My artistic creation consists of piano keyboards, of which each key is another keyboard. I calculated the dimensions that would be necessary to create keyboards with all the same proportions for keyboards with seven keys.I used the API of StdDraw to find ways to draw lines and shapes of different colors to create the keyboards. |
 |
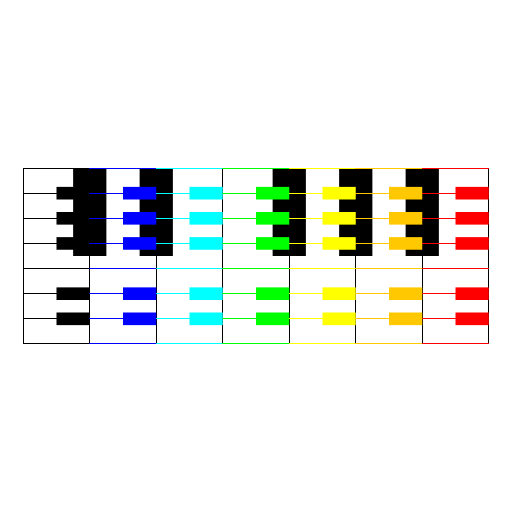 |
 |
 |
 |
 |
Dina Sharon
I drew a Sierpinski carpet which I got from http://library.thinkquest.org/26242/full/fm/fm.html, the website which was mentioned in the checklist. |
 |
 |
 |
 |
 |
 |
Fabrizio Giovannini Filho
My artistic creation consists of a Pythagoras tree. It was invented by Albert E. Bosman in 1942 and is named after the Greek mathematician due to the right triangle that is formed between the squares. First, before programing, I had to find out how the points of each square could be computed from a point of the square of the previous order. I figured out equations for the angles. |
 |
 |
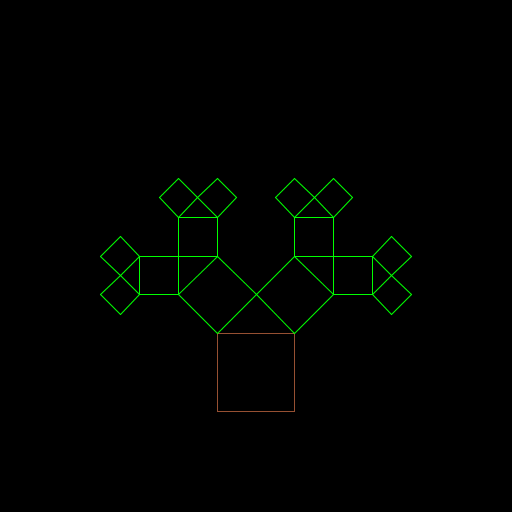 |
 |
 |
 |
Aaron Himelman
My artistic creation consists of a recursive drawing of a hexagon with six lines emanating from its six vertices connected to three smaller hexagons via the three lines on the right. I used geometry to figure out where to place the vertices. It turns out that at a depth of around 7, my art produces a Sierpinski triangle as a result of the overlapping hexagons. |
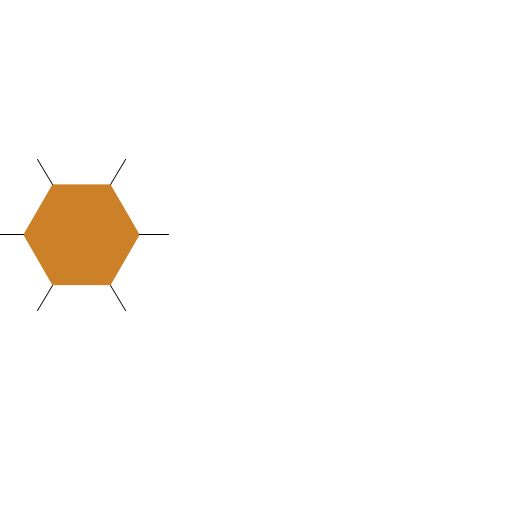 |
 |
 |
 |
 |
 |
Nicola Babarcich
My artistic creation is a recreation of the house attached to balloons from the Disney-Pixar movie "Up". My program used recursion to grow the bunch of balloons and have them vary in placement, size, and length. |
 |
 |
 |
 |
 |
 |
Will Taylor
My artistic creation produces N squares, where the side of each square is made of semicircles. I basically just played around a lot until I got what I was looking for. I did spend a bit of time figuring out what the size should be and where I wanted each square to go, though. |
 |
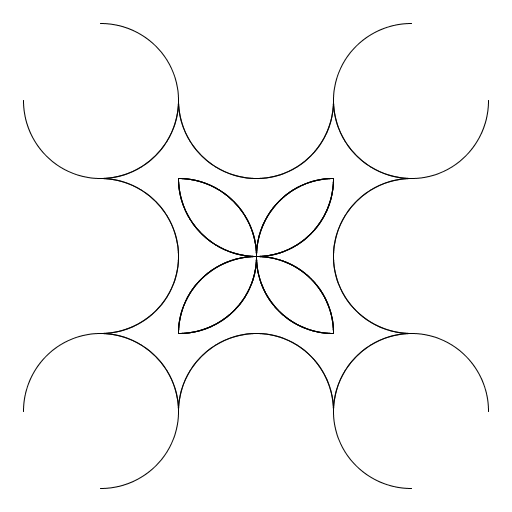 |
 |
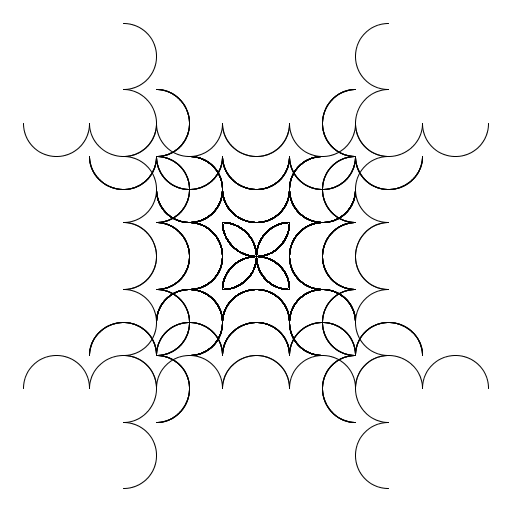 |
 |
 |