| Name and Description ------------------------------------------------- |
N = 1 | N = 2 | N = 3 | N = 4 | N = 5 | N = 6 |
|---|---|---|---|---|---|---|
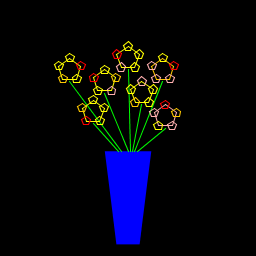
| Cecillia Lui My artistic creation consisted of a vase of flowers. To create the flowers, I used a recursive function that drew a pentagon, and then a pentagon centered at each corner of the original pentagon. I set random equal probabilities to each pentagon drawn to be either pink, orange, red or yellow. Then, I created a function to draw the vase. |
 |
 |
 |
 |
 |
 |
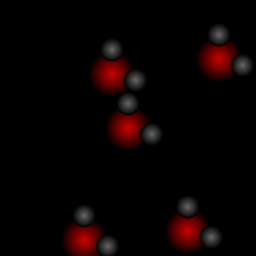
| Jennifer King In order to create each sphere a recursive function "sphere" draws concentric filled circles with a deepening color each time, creating a 3D effect. The recursive function "molecules" creates each individual molecule from three spheres, up to the number of molecules defined by the argument N. The hydrogen atoms are separated by the appropriate bond angle of 104.5 degrees, and all of the atoms are oriented as if there were an electric field moving from the bottom left of the screen to the top right. |
 |
 |
 |
 |
 |
 |
| John Stogin My artistic program was an attempt to emulate snowflake formation. The program starts by drawing a triangle and then drawing triangles starting from the vertices of the first triangle. Each triangle is randomly "rotated" in the third dimension meaning that some of them appear thinner than others. A second random element determines the orientation of the triangle with respect to the previous triangle. Lastly, the program randomly chooses whether or not to continue the recursion for each triangle vertex. |
 |
 |
 |
 |
 |
 |
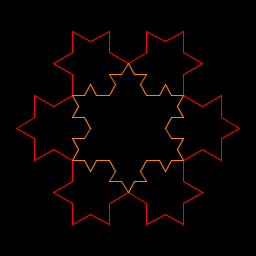
| Kenneth Jenkins My program generates many Koch snowflakes in multiple colors. I wrote a recursive function to draw the pattern, and then decided that it would be neat to draw many nested snowflakes. The nesting bit is non-recursive, but the Koch snowflake pattern is recursive. |
 |
 |
 |
 |
 |
 |
| Katherine Song This creation is a cube that has a Sierpinski carpet design on each face. The colors of the designs are random hues of green. I wrote 3 recursive methods to produce the design on each face. Each method was written to specifically handle the angle of each face. Another method randomly determined which of 10 available shades of green that each tile would be colored. |
 |
 |
 |
 |
 |
 |
| Zack Predmore My artistic creation is a Dragon Curve, a shape that has many interesting properties that I discovered on Wikipedia. It uses two methods that call each other for each level of depth. They work by passing down two arrays of points that represent the vertices of the curve. The formulas for the midpoints are different depending if the starting line has a positive or negative slope. Each time the methods are called, the arrays double in size, so it takes twice as long as the previous call to draw the shape. |
 |
 |
 |
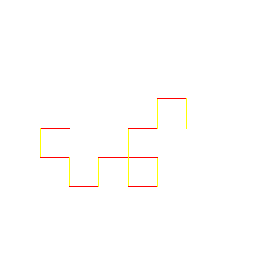 |
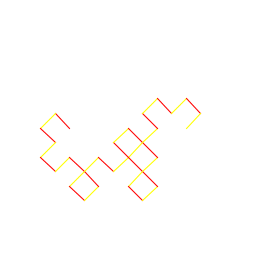 |
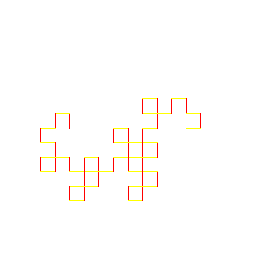 |
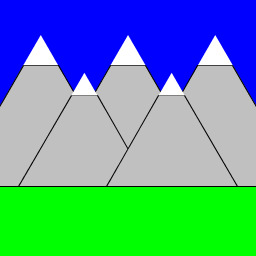
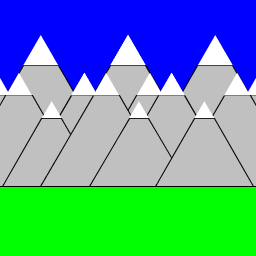
| Cam Ritchie I produced an ever-expanding mountain range, with the allusion of depth. I do this by expanding the range to the left and right and also by putting smaller mountains in front of the larger ones. I wrote multiple recursion loops that create the left, right and two smaller mountains for each existing mountain. |
 |
 |
 |
 |
 |
 |
| Justin Cahill I created "fractal fish"--an image of a big fish eating two smaller fish, who each are eating two smaller fish, etc. The fish required some complex components, including the tail, body, mouth, and eye. |
 |
 |
 |
 |
 |
 |
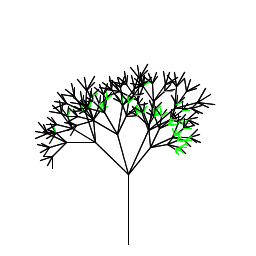
| Elizabeth Nadelman My creation is a tree similar to the picture at the beginning of Chapter 2.3 in the book. Most calculations involved simple trig and adding and subtracting angles. I played with the colors so that it looked more tree-like. As N goes from 0 to 7, the tree grows from a single stem to a large tree with green leaves and red berries (or flowers). |
 |
 |
 |
 |
 |
 |
| Guannan R. Wang My program generates a recursive landscape that consists of rolling mountains, a sun, and a flock of birds. My birds are made of intersecting arcs which makes a more natural shape. |
 |
 |
 |
 |
 |
 |
| Genia Dubrovsky This program first draws a large circle, and then with each level of recursion, it draws smaller circles around the perimeter of the previous circle. The new ci rcles get proportionally smaller as they go around the bigger one, until there i s just a dot at the very back. I also made sure that they would orient themselve s with the largest circle in each group facing away from the center (0, 0). The colors alternate between red and blue. |
 |
 |
 |
 |
||
| David Sprunger I noticed Sierpinski.java without the border eventually approximated a triangle with the border. I decided to try to approximate the circle with polygons, but I thought that would be too simple. So I played around with patterns I could make with diamonds approximating the circle and eventually struck on this one. The geometry wasn't too bad; you just need to know the power of a point theorem to figure out what the diamond's dimensions should be. Around N = 6, 7, or 8 I really like the pattern. Beyond that, there isn't much more visible detail. |
 |
 |
 |
 |
 |
 |
| Michael Adelson This program draws a pattern of rotated squares. The pattern is drawn twice, creating an upper and lower branch. Each recursive call creates a new spiral of squares with a given size ratio from a given corner of the initial square. Tail-end recursion creates another pattern inside each square. The colors alternate based on n, the coordinates are transformed with linear algebra methods. Finally, I got the program to run somewhat faster by stopping a recursion branch not only if n is zero but if the squares are too small to see. |
 |
 |
 |
 |
 |
 |
| M Capece My program produces a recursive hexagonal pattern. With each increasing N three smaller hexagons are placed neatly along the inner edges of the larger hexagon. There is a non-recursive function that makes one regular convex hexagon Also, I changed the colors of the hexagons and the background to make it look more interesting. |
 |
 |
 |
 |
 |
 |
| Sarah Cornfeld This program draws a tree recursively using the draw functions and trigonometric ratios. It ultimately creates a tree with a blue trunk and red leaves. |
 |
 |
 |
 |
 |
 |
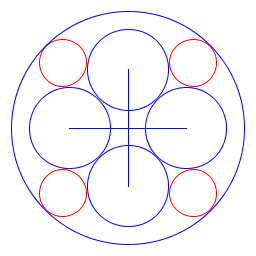
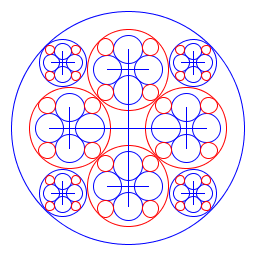
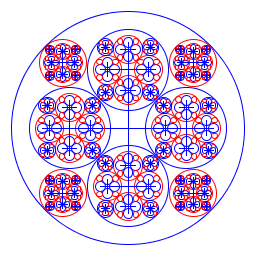
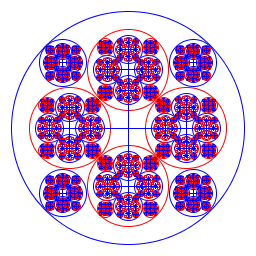
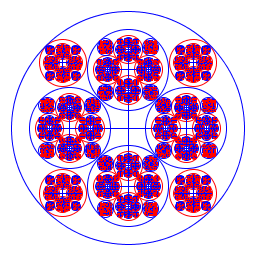
| Alicia Kollar I made a recursive image which alternates color with each recursion. The image repeats itself inside each of the 8 inner circles. In the end it looks somewhat like a huge rose window. I defined my ratios with trial and error. I used the powers of minus one to alternate colors. |
 |
 |
 |
 |
 |