Write a program to decipher messages encoded using a prefix code, given the encoding tree. Such codes are widely used in applications that compress data, including JPEG for images and MP3 for music.

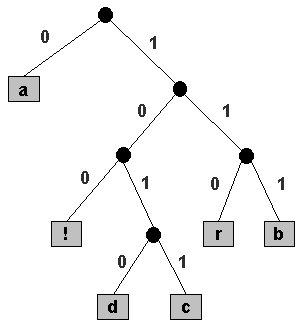
Prefix codes.  A prefix code is most easily represented by a binary tree in which the external nodes are labeled with single characters that are combined to form the message. The encoding for a character is determined by following the path down from the root of the tree to the external node that holds that character: a 0 bit identifies a left branch in the path, and a 1 bit identifies a right branch. In the following tree, black circles are internal nodes and gray squares are external nodes. The code for b is 111, because the external node holding b is reached from the root by taking 3 consecutive right branches. The other codes are given in the table below.

character encoding ------------------- a 0 b 111 c 1011 d 1010 r 110 ! 100

Note that each character is encoded with a (potentially) different number of bits. In the example above, the character 'a' is encoded with a single bit, while the character 'd' is encoded with 4 bits. This is a fundamental property of prefix codes. In order for this encoding scheme to reduce the number of bits in a message, we use short encodings for frequently used characters, and long encodings for infrequent ones.

A second fundamental property of prefix codes is that messages can be formed by simply stringing together the code bits from left to right. For example, the bitstring

0111110010110101001111100100

encodes the message "abracadabra!". The first 0 must encode 'a', then the next three 1's must encode 'b', then 110 must encode r, and so on as follows:

|0|111|110|0|1011|0|1010|0|111|110|0|100
 a  b   r  a  c   a  d   a  b   r  a  !

The codes can be run together because no encoding is a prefix of another one. This property defines a prefix code, and it allows us to represent the character encodings with a binary tree, as shown above. To decode a given bit string:

Representing the binary tree.  To decode a bit string, you need the binary tree that stores the character encodings. We use the preorder traversal of the binary tree to represent the tree itself. Internal nodes are labeled with the special character '*'. (We will restrict ourselves to messages that do not contain this special character.) The preorder traversal of the above tree is:

* a * * ! * d c * r b 

Input format.  The input will consist of the preorder traversal of the binary tree, followed immediately by the compressed message. For the example above, the input file is abra.pre:

*a**!*dc*rb 
0111110010110101001111100100

Part 1: Building the tree.  Write a (recursive) function maketree() that reads in the preorder traversal and reconstructs the corresponding tree. Use the standard binary tree data type below to represent the tree.

typedef struct node *link;
struct node {
   char character;
   link left;
   link right;
};

Part 2: Tree traversal.  Write a function length() that traverses the binary tree, and prints a list of characters in the tree, and the length (number of bits) of their encoding. For the example above, your program should produce the following output (although it need not produce it in this exact ordering):

character  bits
---------------
   a        1
   !        3
   d        4
   c        4
   r        3
   b        3

Part 3: Decoding.  Write a function uncompress() that reads the compressed message from standard input, and writes the uncompressed message to standard output. It should also display the number of bits read in, the number of characters in the original message, and the compression factor.

For example, the original message above contains 12 characters which would normally requires 96 bits of storage (8 bits per character). The compressed message uses only 28 bits, or 29% of the space required without compression. The compression factor depends on the frequency of characters in the message, but ratios around 50% are common for English text. Note that for large messages the amount of space needed to store the description of the tree is negligible compared to storing the message itself, so we have ignored this quantity in the calculation. Also, for simplicity, the compressed message is a sequence of the characters '0' and '1'. In an actual application, these bits would be packed eight to the byte, thus using 1/8th the space. For this input, your program should produce the following output:

character  bits
---------------
   a        1
   !        3
   d        4
   c        4
   r        3
   b        3

abracadabra!
Number of bits       = 28
Number of characters = 12
Compression ratio    = 29.2%

Submission.  Name your program uncompress.c, and submit it along with a readme file.

Extra credit.  In addition to printing out the decoded message, print out the code table itself. That is, for each external node in the tree, print the character followed by its bit encoding. For example:

character  bits  encoding
-------------------------
   a        1     0
   !        3     100
   d        4     1010
   c        4     1011
   r        3     110
   b        3     111

abracadabra!
Number of bits       = 28
Number of characters = 12
Compression ratio    = 29.2%