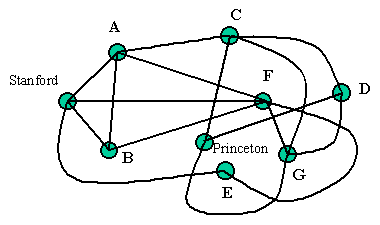
Problem 1
One of the original design goals of ARPANET, the precursor
of the Internet, was that it should be fault-tolerant and
able to survive incidents
that destroyed parts of it. In that spirit, here is a
fake network with routers (the circles) and links between them
(the lines):

(a) What is the smallest set of links that you would have to destroy to disconnect "Princeton" from "Stanford"? List the links by their endpoints, for example A-B or Stanford-F.
You can do it by destroying two links: A-C and F-G.
(b) If a router is destroyed, any link connected to it no longer works. What is the smallest set of routers that you would have to destroy to disconnect "Princeton" from "Stanford" (not including Stanford or Princeton themselves)? List the routers by letter.
You can destroy two routers, F and C.
(c) What routers are two "hops" away from Princeton? That is, what routers can you reach from Princeton by going through exactly two links?
Here is a list, with each router on the list followed by a two-hop path from Princeton to it (there are other two-hop paths to some of these routers): A (Princeton-C-A), C (Princeton-G-C), D (Princeton-C-D), F (Princeton-G-F), G (Princeton-C-G).
(d) What is the shortest path (that is, the path with the fewest links) from Princeton to Stanford? Give the list of routers that make up the path.
The shortest path requires three hops. One three-hop path is Princeton-C-A-Stanford.
(e) What is the longest path from Princeton to Stanford that doesn't have a loop, that is, that doesn't go through any router more than once?
There is an eight-hop path, which visits every router once: Princeton-D-G-C-A-B-F-E-Stanford.
Problem 2
For many years now, the number of computers on the Internet has roughly
doubled every year. Will this trend keep on going forever, or will it
eventually stop? If you think it will go on forever, explain why. If you
think it will stop, give a guesstimate of when it will stop and why.
(Assume that there are about 100 million computers on the Internet now.)
It probably has to stop, because there is some reasonable limit on how many computers per person will exist. If we assume that no more than (say) 1000 computers per person can reasonably exist, then there is a limit of about 6 trillion computers. That's about 60,000 times as many computers as now. Since 60,000 is about 2 to the 16th power, sixteen doublings are required to reach the limit. With one doubling per year, that's about sixteen years from now.
[Note that there is a wide range of right answers to this problem. You might assume that computers will be put out into the world to monitor it; then there might be a limit on the number of computers per square mile, or square foot. Or you might assume that people will come up with every more clever ways of using computers, and the number of computers has no limit. Any well-explained answer is fine.]
Problem 3
The University's library contains about five million books. Assume that
each book contains about ten million bits of information.
(a) How many total bits of information does the library contain?
5 million, times ten million, equals 50 trillion.
(b) How long would it take to download the entire contents of the library over a modem connection running at 50,000 bits per second?
50 trillion, divided by 50,000, equals 1 billion seconds. Divide by 3600 seconds/hour to get 277,777 hours. Divide by 24 hours/day to get 11,574 days. Divide by 365 days/year to get about 31 years.
(c) How long would it take to download the entire contents of the library over a Dormnet connection running at 10,000,000 bits per second?
50 trillion, divided by 10 million, equals 5 million seconds. Divide by 3600 seconds/hour to get 1389 hours. Divide by 24 hours/day to get 58 days, or about two months.
(d) How long would it take to download the entire contents of the library over a "gigabit ethernet" connection at 1,000,000,000 bits per second?
50 trillion, divided by 1 billion, equals 50,000 seconds. Divide by 3600 seconds/hour to get about 14 hours.
Problem 4
Consider your answer to problem 3d, under the assumption that everybody will
have a gigabit ethernet connection to their home in a few years. How do
you think this affects the future of libraries and librarians?
If you can download the entire contents of the library to your home in 14 hours, you won't need to take a trip to the library to view its contents. This has several consequences: