
WordNet is a semantic lexicon for the English language that computational linguists and cognitive scientists use extensively. For example, WordNet was a key component in IBM's Jeopardy-playing Watson computer system. WordNet groups words into sets of synonyms called synsets. For example, { AND circuit, AND gate } is a synset that represent a logical gate that fires only when all of its inputs fire. WordNet also describes semantic relationships between synsets. One such relationship is the is-a relationship, which connects a hyponym (more specific synset) to a hypernym (more general synset). For example, the synset { gate, logic gate } is a hypernym of { AND circuit, AND gate } because an AND gate is a kind of logic gate.
The WordNet digraph. Your first task is to build the WordNet digraph: each vertex v is an integer that represents a synset, and each directed edge v→w represents that w is a hypernym of v. The WordNet digraph is a rooted DAG: it is acyclic and has one vertex—the root—that is an ancestor of every other vertex. However, it is not necessarily a tree because a synset can have more than one hypernym. A small subgraph of the WordNet digraph appears below.

The WordNet input file formats. We now describe the two data files that you will use to create the WordNet digraph. The files are in comma-separated values (CSV) format: each line contains a sequence of fields, separated by commas.


WordNet data type. Implement an immutable data type WordNet with the following API:
public class WordNet {
// constructor takes the name of the two input files
public WordNet(String synsets, String hypernyms)
// all WordNet nouns
public Iterable<String> nouns()
// is the word a WordNet noun?
public boolean isNoun(String word)
// a synset (second field of synsets.txt) that is a shortest common ancestor
// of noun1 and noun2 (defined below)
public String sca(String noun1, String noun2)
// distance between noun1 and noun2 (defined below)
public int distance(String noun1, String noun2)
// do unit testing of this class
public static void main(String[] args)
}
Corner cases.
All methods and the constructor should throw a
java.lang.NullPointerException if any argument is null.
The distance() and sca() methods
should throw a java.lang.IllegalArgumentException
unless both of the noun arguments are WordNet nouns.
You may assume that the input files are in the specified format (and that the underlying
digraph is a rooted DAG).
Performance requirements. Your data type should use space linear in the input size (size of synsets and hypernyms files). The constructor should take time linearithmic (or better) in the input size. The method isNoun() should run in time logarithmic (or better) in the number of nouns. The methods distance() and sca() should make exactly one call to the length() and ancestor() methods in ShortestCommonAncestor, respectively. For the analysis, assume that the number of characters in a noun or synset is bounded by a constant.
Shortest common ancestor. An ancestral path between two vertices v and w in a rooted DAG is a directed path from v to a common ancestor x, together with a directed path from w to the same ancestor x. A shortest ancestral path is an ancestral path of minimum total length. We refer to the common ancestor in a shortest ancestral path as a shortest common ancestor. Note that a shortest common ancestor always exists because the root is an ancestor of every vertex. Note also that an ancestral path is a path, but not a directed path.

We generalize the notion of shortest common ancestor to subsets of vertices. A shortest ancestral path of two subsets of vertices A and B is a shortest ancestral path over all pairs of vertices v and w, with v in A and w in B. The figure below shows an example in which, for two subsets, red and blue, we have computed several (but not all) ancestral paths, including the shortest one.
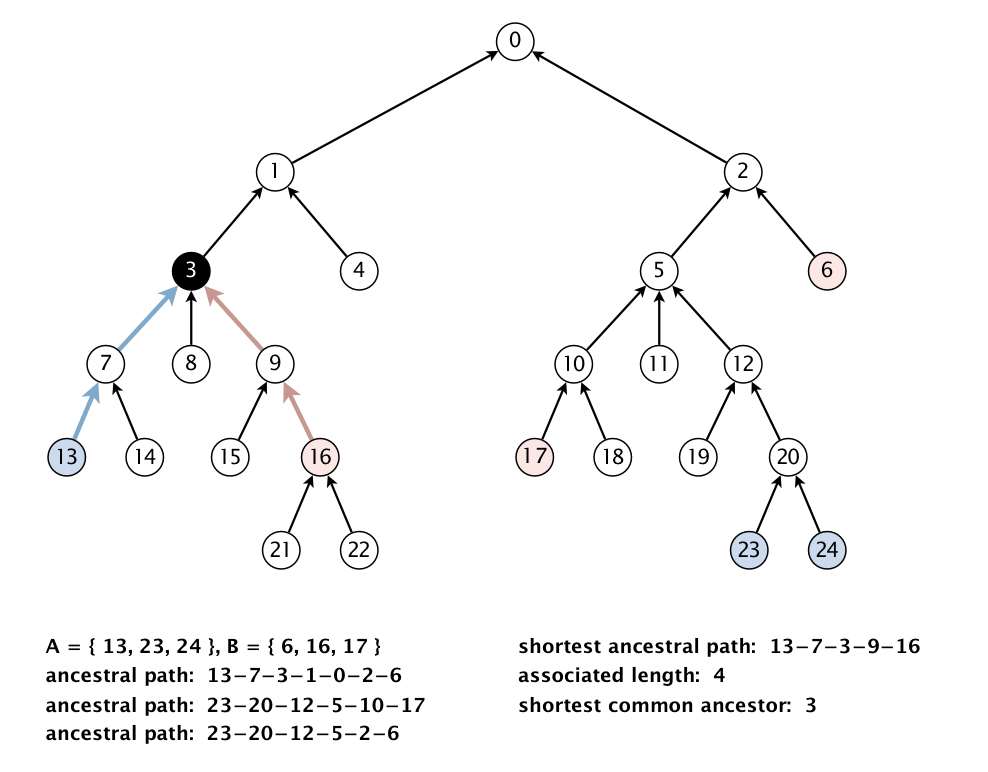
Shortest common ancestor data type.
Implement an immutable data type ShortestCommonAncestor with the following API:
public class ShortestCommonAncestor {
// constructor takes a rooted DAG as argument
public ShortestCommonAncestor(Digraph G)
// length of shortest ancestral path between v and w
public int length(int v, int w)
// a shortest common ancestor of vertices v and w
public int ancestor(int v, int w)
// length of shortest ancestral path of vertex subsets A and B
public int length(Iterable<Integer> subsetA, Iterable<Integer> subsetB)
// a shortest common ancestor of vertex subsets A and B
public int ancestor(Iterable<Integer> subsetA, Iterable<Integer> subsetB)
// do unit testing of this class
public static void main(String[] args)
}
Corner cases. All methods and the constructor should throw a java.lang.NullPointerException if any argument is null or if any iterable argument contains a null item. The constructor should throw a java.lang.IllegalArgumentException if the digraph is not a rooted DAG. The methods length() and ancestor() should throw a java.lang.IndexOutOfBoundsException if any argument vertex is invalid and a java.lang.IllegalArgumentException if any iterable argument contains zero vertices.
Basic performance requirements. Your data type should use space proportional to E + V, where E and V are the number of edges and vertices in the digraph, respectively. All methods and the constructor should take time proportional to E + V (or better).
Additional performance requirements. For extra credit, in addition, the methods length() and ancestor() should take time proportional to the number of vertices and edges reachable from the argument vertices (or better), For example, to compute the shortest common ancestor of v and w in the digraph below, your algorithm can examine only the highlighted vertices and edges and it cannot initialize any vertex-indexed arrays.

Test client. The following test client takes the name of a digraph input file as as a command-line argument, creates the digraph, reads in vertex pairs from standard input, and prints the length of the shortest ancestral path between the two vertices along with a shortest common ancestor:
public static void main(String[] args) {
In in = new In(args[0]);
Digraph G = new Digraph(in);
ShortestCommonAncestor sca = new ShortestCommonAncestor(G);
while (!StdIn.isEmpty()) {
int v = StdIn.readInt();
int w = StdIn.readInt();
int length = sca.length(v, w);
int ancestor = sca.ancestor(v, w);
StdOut.printf("length = %d, ancestor = %d\n", length, ancestor);
}
}