This exercise will be live-coded during the class meeting.
\(H(n, r) = \frac{1}{1^r} + \frac{1}{2^r} + \cdots + \frac{1}{n^r}.\)For example, \(H(3, 1) = \frac{1}{1^1} + \frac{1}{2^1} + \frac{1}{3^1} = \frac{11}{6} \approx 1.833333\) and \(H(3, 2) = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} = \frac{49}{36} \approx 1.361111\).
Note: you may assume that n is a positive integer.
Hint: use Math.pow(x, y) to raise x to the power y.
Remark: the generalized harmonic numbers are closely related to the Riemann zeta function, which plays a central role in number theory.
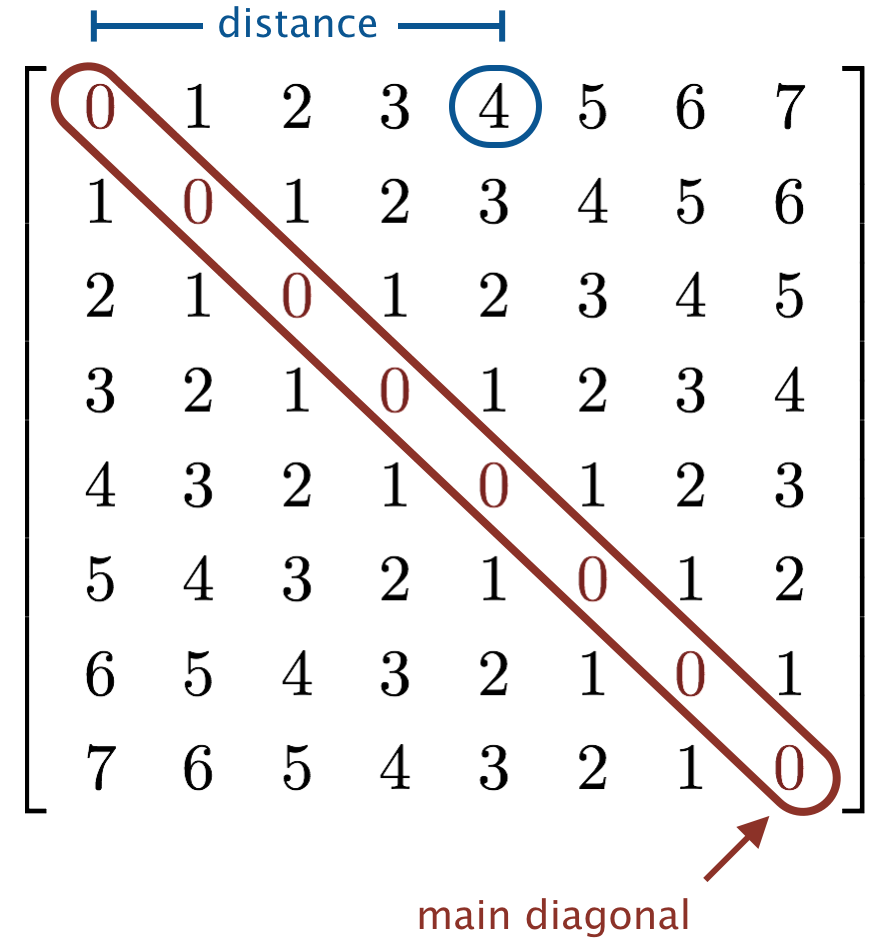
Note: you may assume that n and width are nonnegative integers.
Hint 1: Do not use arrays.
Hint 2: Devise an expression that determines the distance of element (i, j) from the main diagonal. For reference, the following diagram illustrates the distance of each element in an 8-by-8 matrix. Solution to hint.
Remark: band matrices are matrices whose nonzero entries are restricted to a diagnonal band. They arise frequently in numerical linear algebra.