








My program can also find the eigenvectors of the laplacian matrix. Since the cotangent laplacian matrix is not symmetric, for this feature I use the connectivity laplacian matrix instead.
I use the reverse communication interface of ARPACK++ to implement this feature.
Here I demonstrate the smallest non-zero eigenvectors of dragon, armadillo, and bunny meshes. We can observe that the eigenvectors with smallest eigenvalues encode low-frequency information, and eigenvectors with larger eigenvalues encode higher-frequency information.
| Index | Eigenvector |
|---|---|
| 1 |  |
| 2 |  |
| 3 |  |
| 4 |  |
| 5 |  |
| 7 |  |
| 14 |  |
| 18 |  |
| 122 |  |
| Index | Eigenvector |
|---|---|
| 1 |  |
| 2 |  |
| 3 |  |
| 4 |  |
| 5 |  |
| 97 |  |
| 103 |  |
| Index | Eigenvector |
|---|---|
| 1 |  |
| 2 |  |
| 3 |  |
| 4 |  |
| 5 | 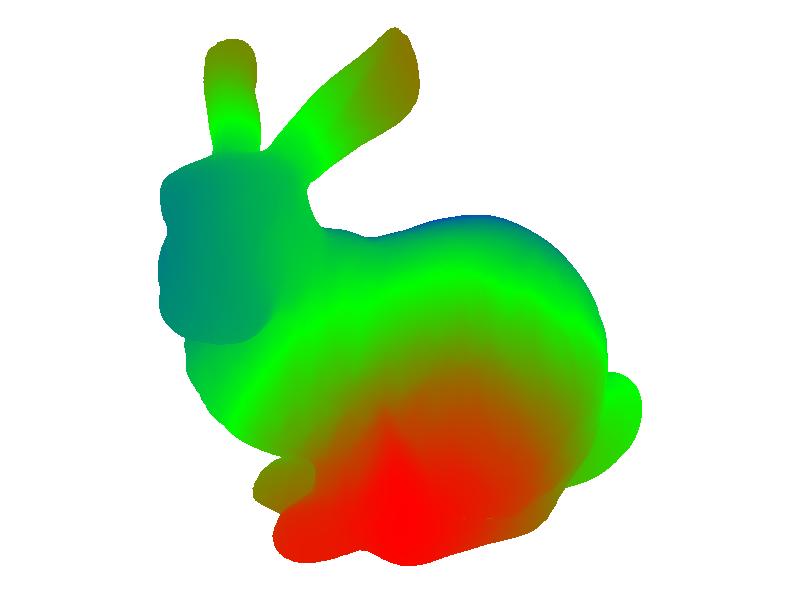 |
| 24 | 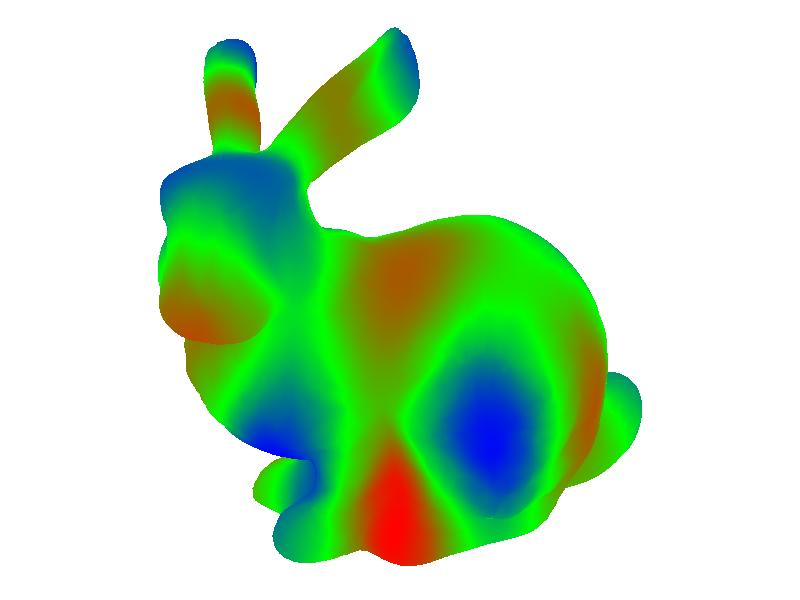 |
| 39 |  |