Write a program to simulate plucking a guitar string using the Karplus-Strong algorithm. This algorithm played a seminal role in the emergence of physically modeled sound synthesis (where a physical description of a musical instrument is used to synthesize sound electronically).

Digital audio. Before reading this assignment, review the material in the textbook on digital audio (pp. 147–151, 202–206).

Simulate the plucking of a guitar string. When a guitar string is plucked, the string vibrates and creates sound. The length of the string determines its fundamental frequency of vibration. We model a guitar string by sampling its displacement (a real number between -1/2 and +1/2) at N equally spaced points (in time), where N equals the sampling rate (44,100) divided by the fundamental frequency (where the quotient is rounded to the nearest integer).

• Plucking the string. The excitation of the string can contain energy at any frequency. We simulate the excitation by filling the buffer with white noise: set each of the N sample displacements to a random real number between -1/2 and +1/2.

  

• The resulting vibrations. After the string is plucked, the string vibrates. The pluck causes a displacement which spreads wave-like over time. The Karplus-Strong algorithm simulates this vibration by maintaining a ring buffer of the N samples: the algorithm repeatedly deletes the first sample from the buffer and adds to the end of the buffer the average of the first two samples, scaled by an energy decay factor of 0.996.

  

Why it works? The two primary components that make the Karplus-Strong algorithm work are the ring buffer feedback mechanism and the averaging operation.

• The ring buffer feedback mechanism. The ring buffer models the medium (a string tied down at both ends) in which the energy travels back and forth. The length of the ring buffer determines the fundamental frequency of the resulting sound. Sonically, the feedback mechanism reinforces only the fundamental frequency and its harmonics (frequencies at integer multiples of the fundamental). The energy decay factor (.996 in this case) models the slight dissipation in energy as the wave makes a roundtrip through the string.

• The averaging operation. The averaging operation serves as a gentle low-pass filter (which removes higher frequencies while allowing lower frequencies to pass, hence the name). Because it is in the path of the feedback, this has the effect of gradually attenuating the higher harmonics while keeping the lower ones, which corresponds closely with how actually plucked strings sound.

Ring buffer. Your first task is to create a data type to model the buffer. Write a class named RingBuffer that implements the following API:

public class RingBuffer
-----------------------------------------------------------------------------------------
        RingBuffer(int capacity)  // create an empty ring buffer, with given max capacity
    int size()                    // return number of items currently in the buffer
boolean isEmpty()                 // is the buffer empty (size equals zero)?
boolean isFull()                  // is the buffer full  (size equals capacity)?
   void enqueue(double x)         // add item x to the end
 double dequeue()                 // delete and return item from the front
 double peek()                    // return (but do not delete) item from the front

Implement RingBuffer to throw an exception if the client attempts to dequeue() from an empty buffer or enqueue() into a full buffer to indicate the error.

Guitar string. Next, create a data type to model a vibrating guitar string. Write a class named GuitarString that implements the following API:

public class GuitarString
------------------------------------------------------------------------------------------------------------------------
       GuitarString(double frequency)  // create a guitar string of the given frequency, using a sampling rate of 44,100
       GuitarString(double[] init)     // create a guitar string whose size and initial values are given by the array
  void pluck()                         // set the buffer to white noise
  void tic()                           // advance the simulation one time step
double sample()                        // return the current sample
   int time()                          // return number of tics

• Constructors. There are two ways to create a GuitarString object.

  • The first constructor creates a RingBuffer of the desired capacity N (sampling rate 44,100 divided by frequency, rounded to the nearest integer), and initializes it to represent a guitar string at rest by enqueueing N zeros.

  • The second constructor creates a RingBuffer of capacity equal to the size of the array, and initializes the contents of the buffer to the values in the array. On this assignment, its main purpose is for debugging and grading.

• Pluck. Replace the N elements in the buffer with N random values between -0.5 and +0.5.

• Tic. Apply the Karplus-Strong update: delete the sample at the front of the buffer and add to the end of the buffer the average of the first two samples, multiplied by the energy decay factor.

• Sample. Return the value of the item at the front of the buffer.

• Time. Return the total number of times tic() was called.

Interactive guitar player. GuitarHeroLite.java is a sample client (of GuitarString.java, StdDraw.java, and StdAudio.java) that plays the guitar in real-time, using the keyboard to input notes. When the user types the lowercase letter 'a' or 'c', the program plucks the corresponding string. Since the combined result of several sound waves is the sum of the individual sound waves, we play the sum of all string samples.

public class GuitarHeroLite { public static void main(String[] args) { // create two guitar strings, for concert A and C double CONCERT_A = 440.0; double CONCERT_C = CONCERT_A * Math.pow(2, 3.0/12.0); GuitarString stringA = new GuitarString(CONCERT_A); GuitarString stringC = new GuitarString(CONCERT_C); while (true) { // check if the user has typed a key; if so, process it if (StdDraw.hasNextKeyTyped()) { char key = StdDraw.nextKeyTyped(); if (key == 'a') { stringA.pluck(); } else if (key == 'c') { stringC.pluck(); } } // compute the superposition of samples double sample = stringA.sample() + stringC.sample(); // play the sample on standard audio StdAudio.play(sample); // advance the simulation of each guitar string by one step stringA.tic(); stringC.tic(); } } }

String keyboard = "q2we4r5ty7u8i9op-[=zxdcfvgbnjmk,.;/' ";

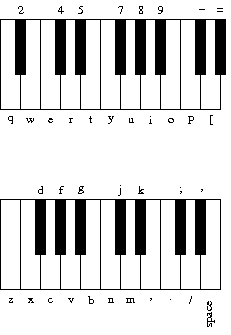
Submission.   Submit RingBuffer.java, GuitarString.java, and GuitarHero.java. Finally, submit a readme.txt file and answer the questions.

Extra credit 1. Write a program GuitarHeroVisualizer.java (by modifying GuitarHero.java) that plots the sound wave in real-time, as the user is playing the keyboard guitar. The output should look something like this, but change over time.

Extra credit 2. Bring your laptop to precept and perform a piece for your classmates. Partners may perform a duet and both will receive extra credit, or a solo for individual extra credit.

Challenge for the bored. Modify the Karplus-Strong algorithm to synthesize a different instrument. Consider changing the excitation of the string (from white-noise to something more structured) or changing the averaging formula (from the average of the first two samples to a more complicated rule) or anything else you might imagine.