Minimum-Distance Classifiers

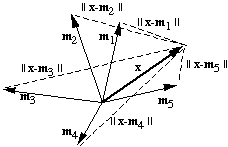
Template matching can easily be expressed mathematically. Let x be the feature vector for the unknown input, and let m₁, m₂, ..., m_c be templates (i.e., perfect, noise-free feature vectors) for the c classes. Then the error in matching x against m_k is given by

|| x - m_k || .

Here || u || is called the norm of the vector u. A minimum-error classifier computes || x - m_k || for k = 1 to c and chooses the class for which this error is minimum. Since || x - m_k || is also the distance from x to m_k, we call this a minimum-distance classifier. Clearly, a template matching system is a minimum-distance classifier.

Back to Templates On to Metrics Up to Simple Classifiers