| Name and Description | N = 1 | N = 2 | N = 3 | N = 4 | N = 5 |
|---|---|---|---|---|---|
| Thompson/Jeffrey Philip P01B, My program draws a solid composed of tetrahedrons. The base case (N = 0) is simply a tetrahedron. Each additional level of recursion generates four children. (At all levels below the first, one of the four children is not visible because it ends up inside the tetrahedron two levels higher.) |
 |
 |
 |
 |
 |
| /Schulam/Peter Franz P03, My artistic creation creates a grape vine. To create a triangular bunch of grapes, I have a recursive function to create the actual bunch of grapes with calls to an individual grape function. I also have a recursive function, vine, that draws two stems emerging from each bunch of grapes. |
 |
 |
 |
 |
 |
| Clayton Schwarz B01, Basically this program draws a scene with a recursively defined fire in the foreground, a recursively defined horizon in the background, and stars in the sky which include bigger stars that are essentially recursively defined constellations. For each of these examples, I choose values for the recursive aspects of the picture, generally in increasing depth of recursion as you go from 0 to 7. |
 |
 |
 |
 |
 |
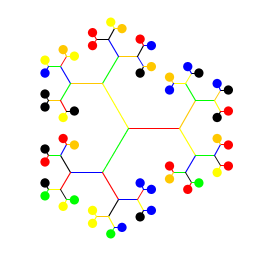
| /Dietz IV/Donald Elmore P03, While walking home from class one day, I saw someone wearing an argyle sweater, so I was inspired to write a program that draws a sweater and then draws a recursive argyle pattern in the middle of it. I alternate the colors by assigning a fixed color to diamonds in a fixed relative location (that is, gray is always on the left, red in the middle, green on the bottom, etc.). I drew and mapped the coordinates of the vertices for a sweater-shaped polygon and initialized two arrays to store the values for its vertices. |
 |
 |
 |
 |
 |
| Finkelstein/Eric Neal P03, I created a face with features made out of snowflakes. For even N it smiles and for odd it frowns. The COS website suggested making a snowflake by erasing sides of equilateral triangles, but I found it easier to "erase" the snowflakes by letting their uniform whiteness only allow the outline to show. |
 |
 |
 |
 |
 |
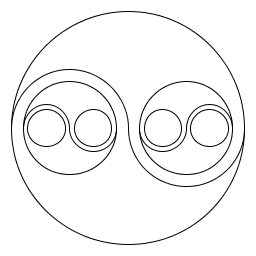
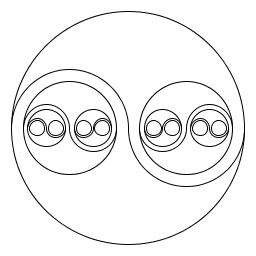
| Gray/Gabriel J/ P03, The program produces a recursive yinYang picture. It is created by filling the "eyes" of the classical yinYang picture. Note that the open "eye" is not outlined for aesthetic reasons. The main method draws 2 semicircles, dividing the current circle into the two yinYang regions. The recursive method then draws a circle where the classical filled "eye" of the yingYang image would go, and a recursive call to draw the reflection of the above described YingYang image in the opposing open circle. |
 |
 |
 |
 |
 |
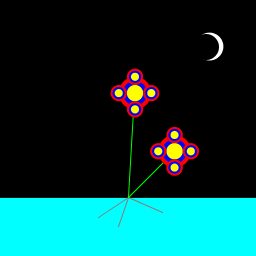
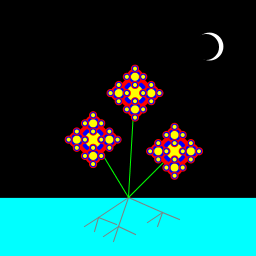
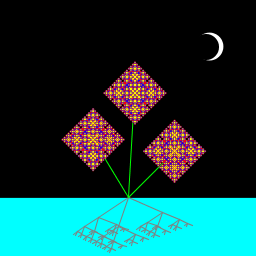
| Peters/Niklas Stewart P02, My program depicts a flower growing in the sea at night. A single flower lands on the water and then sets down roots and simultaneously duplicates itself. Three flowers end up growing from the single plant. During each step the number of roots increases and the flowers become more elaborate. |
 |
 |
 |
 |
 |
| 10/Rucinski/Christopher Thomas P01A, I use a Tetris shape as my "base" shape. Realizing that each T had three children, and that there were three components to each color in the RGB method of representing color, I decided to increase the saturation of each child, depending on its relative location to the parent. The result is, I think, quite fascinating, especially around the range of 10 or so levels of recursion, when the pattern becomes more defined and the figure has a rather fluorescent look about it. My program draws three Tetris Ts within a T in a recursive manner. Figuring out where to draw the Ts was challenging since orientation was an issue. |
 |
 |
 |
 |
 |
| 11/Hadzhieva/Sonya Atanasova P01A, My artistic creation is the "Recursive tree" from the Creative exercises from chapter 2.3, Recursions, in the textbook. I tried to make a tree similar to the one shown in the textbook but I chose the initial angles that the branches are rotated and used an angle alpha in the recursion function. I used trigonometric equations to define the positions of the new branches. |  |
 |
 |
 |
 |
| 11/Pondicherry/Tarun P02, My program creates a fractal using the Princeton shield and generates a tiger head image when N > 6. Step 1: Created drawShield function to create a shield using polygons. Step 2: Created transformPoints function to translate and rotate the shield. Step 3: Created recursive art function and manually adjusted scaling parameters to create a pattern without too much space or overlap. Step 4: Changed the transparency of different depth levels to improve the look of the fractal generated. After trying various combinations and observing their result, I noticed that a tiger head is generated by the fractal. I then tweaked some of the constants to make the tiger head image as noticeable as possible. |
 |
 |
 |
 |
 |
| 11/Hsu/Yu-han Huang/ B02, My program draws a flower that has increasing layers of petals as the depth of the recursion increases. First, I wrote two functions that would draw the petals of the flower at different angles and which are used alternately, so 1 group of petals would seem to rotate by 30 degrees from the previous group. At each recursive level, the function draws both an outer layer and an inner layer of petals. Finally, I inserted 2 different sets of arc sizes and angles so the shape of the flower would be different for even and odd n. |
 |
 |
 |
 |
 |
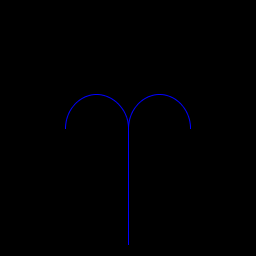
| Adam Hesterberg P04A, The program draws a tree in which every vertex has degree 3, except the leaves, which are circles. If a probability is entered before the depth, then each branch continues as before with that probability, or otherwise ends. |
 |
 |
 |
 |
 |
| Carlton Chow P04A, This program draws "branches" of two tangent semi-circles. It provides different coloring for each new "layer" or dimension of semi-circles, based on the # of the layer and it's factorization. I made the semi-circles half the radius after each layer, so that the smaller and smaller circles will eventually reach, but never overlap, the two original semi-circles diameters on the inside, and a length equal to 1 diameter on each side of the original semi-circles. |
 |
 |
 |
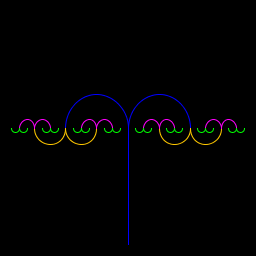 |
 |
| Mendy Fisch P04A, My artistic creation is a recursive design made out of orange and black Ps. Each P has four smaller Ps inside of it. If N is odd, the first level will be black, the second orange, etc. If N is even, it is the other way around. In order to draw the Ps, I positioned a filled rectangle and two filled circles so that they made a P shape together. For color variation in drawing the Ps, I u sed Math.random to generate numbers for colors that would either be in the orange range or the balck/gray range. I also used Math.random to slightly vary the alpha for the white in the middle of the Ps, so sometimes that looks slightly gray. |
 |
 |
 |
 |
 |
| Max Rosmarin P04A, It is a domino fractal: a set of dominoes whose "dots" are actually smaller dominoes, etc. to a certain depth after which the dots are actual dots. The domino drawn is determined randomly (1-6) at each level. |
 |
 |
 |
 |
 |
| Roger Podwysocki P04A, My creation is a fractal curve, similar to the Koch Snowflake, except that I create a triangle on the second half of a line segment rather than on the middle third, and the triangle is not necessarily equilateral. I used some trigonometry because each triangle's orientation is based on the orientation of the line segment it is made from. My original conception of the curve was that it would look somewhat like a landscape of varying smoothness depending on the number of recursions. |
 |
 |
 |
 |
 |
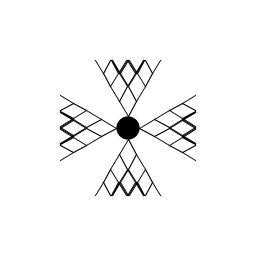
| Nathaniel Roquet B01, My artistic creation is supposed to be an artsy representation of the sun with symmetry and recursive drawings that head north, south, east, and west. I drew a circle at the center of four recursive functions. Each function takes a shape 'V' created with two line segments separated by 60 degrees and redrawn recursively in certain direction (north, south, east, west). The larger the depth written into the command line, the longer and more complex each ray becomes. |
 |
 |
 |
 |
 |
| Ju G. Nam P04A, I first designed a heart figure (by overlapping two circles and one quadrilateral) and used recursion to make a decorative pattern. |
 |
 |
 |
 |
 |
| Berkowitz/Brian Andrew P01, I created a diamond figure. With each recursive depth, I shrunk the figure, changed the color, and placed it on top of the original shape. Then I further shrunk the three-layered design and put it in the corners of the screen. |  |
 |
 |
 |
 |
| Comerford/Peter Pontes de Campos P04, My creation draws a recursive forest. That is, the pattern of trees is recursive, and the trees themselves are recursive. I wrote two recursive functions. Naturally, it's an expensive program, but I think it was worth it. The actual algorithm was straight-forward, but I spent a good deal of time tweaking the values so that it would look nicer. |
 |
 |
 |
 |
 |
| -------------------------------------------------- |
|||||