| Repeats | Diagnosis |
| 0 - 9 | not human |
| 10 - 35 | normal |
| 36 - 39 | high risk |
| 40 - 180 | Huntington's disease |
| 181 - ∞ | not human |
Write a program to read in a human DNA sequence from standard input and identify whether the patient is at risk for HD by determining the maximum number of CAG repeats. Output the maximum number of repeats, and an appropriate medical diagnosis based on the table above. The data file format will consist of a sequence of the letters A, C, G, and T, along with arbitrary amounts of whitespace separating the letters. For full credit, your program should be able to identify CAG repeats that span multiple lines.
For example, the following sequence has a CAG repeat of size 4.
Here is a sample run of your program:TTTTTTTTTTTTTTTTTTTTTTTTTTTTCAGCAGCAG CAGTTTCAGCAGTTTTTTTTTTTTTTTTTTTTTTTTT TTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTT
% java Huntingtons < test1.txt max number of CAG repeats = 4 not human
Use this Turing machine simulator to develop your machine. Your job is to create and submit a text file comparator.tur containing the description of your Turing machine like the one below, but instead of adding the two binary numbers, it should compare them.
title Binary Adder description Add two binary numbers, and leave the result on the tape. vertices 2 R 0.25 0.75 0 L 0.25 0.25 1 L 0.75 0.25 3 L 0.75 0.75 4 R 0.40 0.50 5 H 0.60 0.50 edges 0 0 0 1 135 0 1 1 0 0 4 + # 1 3 + + 2 0 # # 3 2 # 1 0.2 3 2 0 1 -0.2 3 3 1 0 -30 4 4 1 # -135 4 5 # # tapes [1] 0 1 0 + 1 1 1 1 [1] 0 0 + 1 1 1 [1] 1 0 0 + 1 1 [1] 0 1 0 + 1 0 0 1 0 1 |
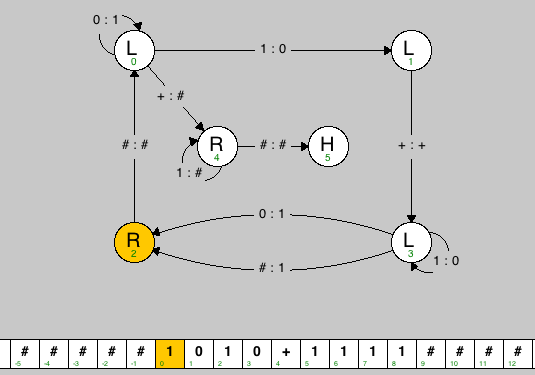 |
The data file is divided into 5 sections (title, description, vertices, edges, tapes), and each section begins with the corresponding name. Each vertex (state) is specified with 4 required values: its name (a string), its type (L, R, Y, N, H), and its x and y coordinates (between 0 and 1). The first state listed is the start state. Each edge (transition) is specified with 4 required values: the starting state, the ending state, the symbol to read, and the symbol to write. An optional 5th parameter specifies the curvature with which to draw the edge (straight line by default). Each tape is specified by listing its symbols, separated by spaces. The tape head starts at the symbol delimited by square braces, which for this assignment should always be the leftmost non-blank character.
Write a function factorize(x) that computes the prime factorization of the long integer x. It should return the factors as an array of long integers. Your function must run in a polynomial number of steps, plus a polynomial number of calls to the subroutine hasFactor. As usual, by polynomial, we mean polynomial in the input size - the number of bits in the binary representation of x.
For testing purposes, include the following (exponential-time) implementation of hasFactor.
public static boolean hasFactor(long x, long y) {
for (long i = 2; i*i <= x && i <= y; i++)
if (x % i == 0) return true;
return false;
}
public static void main(String[] args) {
long x = Long.parseLong(args[0]);
long[] factors = factorize(x);
for (int i = 0; i < factors.length; i++)
System.out.print(factors[i] + " ");
System.out.println();
}
% java Reduction 123456789 3 3 3607 3803