

|
COS 323 - Computing for the Physical and Social Sciences |
Fall 2012 |
| Course home | Outline and lecture notes | Assignments |
Assignment by Niki Kittur, Modified by Roger Ahn and Ken Steiglitz
Due Tuesday, Nov. 27
Chaos has been found in many aspects of the physical world ranging from
the weather to the human heartbeat [Gleick87]. Some concrete
and definable
examples of chaos can be seen in oscillating chemical reactions.
One example is the Belousov-Zhabotinskii reaction in chemistry. By changing the rate at which reactants are fed into the system, the oscillations can change from periodic behavior to chaotic.
The chemistry of the BZ reaction is rather complex, and involves the oxidation of easily brominated organic material by bromate ion in an acidic environment, which makes it rather difficult to model [Baker90, Rowland90, Kapral95].
Slightly simpler is a similar reaction involving a three-variable autocatalator [Peng90]. Autocalators involve isothermal reactions of chemicals in a thermodynamically closed environment - that is, reactions that maintain a constant temperature. Two-variable autocatalators have been successful in reproducing many types of chemical oscillations; a chemical modification by Peng et al. produced a three-variable autocalator which shows complex periodic as well as chaotic behavior. The chemistry of this reaction is as follows: $$P \longrightarrow A$$ $$P+C \longrightarrow A+C$$ $$A \longrightarrow B$$ $$A+2B \longrightarrow 3B$$ $$B \longrightarrow C$$ $$C \longrightarrow D$$
This chemistry can be modeled by the following differential equations: $$ {dA \over dt}=k_1P+k_2PC-k_3A-k_4AB^2 $$ $$ {dB \over dt}=k_3A+k_4AB^2-k_5B $$ $$ {dC \over dt}=k_4B-k_5C $$ This can be converted into the following dimensionless form: $$ {dX \over d\tau}=c_1+c_2Z-X-XY^2 $$ $$ c_3{dY \over d\tau}=X+XY^2-Y $$ $$ c_4{dZ \over d\tau}=Y-Z $$ In the equations above the $c_i$ are constants, and X, Y, and Z are proportional to A, B, and C respectively.
Goal: The "final product" of this assignment is a bifurcation diagram showing the changing behavior of with respect to $c_2$. Jumping in head-first and writing working code that produces impressive bifurcation images in a single session would be a pretty neat trick. The sane experienced programmer, humbled by days of searching for silly mistakes, would follow the baby-steps listed below, since debugging bit-by-bit (excuse the pun) is much easier than troubleshooting the entire program at once. This "baby-steps" methodology is the key to successfully building any program that is made of multiple components [Oz91].
a) Write a Matlab implementation of Euler's method and use it to plot: $$ {dy \over dt}=y \qquad y(0)=1$$ How do your results compare to a graph of $y=e^t$. How does the size of the time steps and number of iterations affect the accuracy of your results?
b) Use Euler's method to plot: $${dy \over dt}=k \cos(t) \qquad y(0)=0 \qquad k=1$$ Compare your results to a graph of $y= \sin(t)$. Again, comment on the effect of varying the time step size and number of iterations.
Save a copy of this code for use in 3a.
The $y$ values plotted in the bifurcation diagram will actually be the peak $\log Y$ values shown against their respective $c_2$ values, which makes this step an integral one.
a) Devise an algorithm to locate the peak $y$-values (local maxima) when $y$ is determined by: $${dy \over dt}=k \cos(t) \qquad y(0)=0 \qquad k=1$$
b) Modify the algorithm so that each peak value is returned only once. Ensure that it will still return all of the peaks of multiple-peak functions like the $y$ determined by: $${dy \over dt}= \cos(t) + \sin(2t) \qquad y(0)=0 \qquad $$ By stopping the same peaks from being returned redundantly, this step serves as an important time saver.
c) Varying k from 1 to 5, plot the peaks of $y$ determined by: $${dy \over dt}=k \cos(t) \qquad y(0)=0 $$ against the changing values of $k$. You should have a straight line stretching from (1,1) to (5,5).
a) Using the code from step 1 and the three autocatalator equations, plot $\log (Y)$ against time. Use the following values for the constants: $$c_1=10 \qquad c_2=0.15 \qquad c_3=0.005 \qquad c_4=0.02$$ You should have an oscillating graph.
b) Using the code from step 2c and the three equations, vary $c_2$ from 0.10 to 0.18 with very small intervals (0.0005 or less), and plot all the peaks of $\log (Y)$ against their respective values of $c_2$. This should yield a birfurcation diagram. You should discard some of the initial peaks you find (i.e., before the system converges to periodic behavior) to get a cleaner diagram.
a) Implement the fourth-order Runge-Kutta method, and use it to plot: $${dy \over dt}=y \qquad y(0)=1 $$ and $${dy \over dt}=k \cos(t) \qquad y(0)=0 \qquad k=1.$$
Compare your results to graphs of $y= \sin(t)$ and $y=e^t$ and those created with Euler's method.
b) Using the code from the previous step and the three autocatalator equations, plot $\log (Y)$ against time. Use the following values for the constants: $$c_1=10 \qquad c_2=0.15 \qquad c_3=0.005 \qquad c_4=0.02 $$ Compare your results with those generated by Euler's Method in 3a.
c) Combine the Runge-Kutta method with your peak-finding algorithm from step 2 to generate a bifurcation diagram similar to that of step 3b. Compare the graphs. Are there any differences?
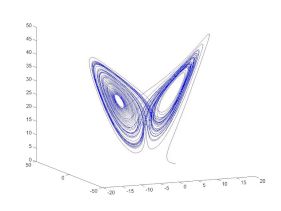
Sample attractor - not necessarily what you'll get...
A strange attractor [Lorenz63] is essentially a graphical representation of $x$, $y$, and $z$, parametrized by time. It is called an attractor because $x$, $y$, and $z$ never stray far from a certain point or points in space. It is considered "strange" because the $x$, $y$, and $z$ may infinitely loop around these points of attraction, yet never repeat itself. Thus if one were to follow a line connecting each point to the next, one would find a line of infinite length within the finite volume of the attractor.
Use Matlab's plot3 command to plot the attractor for $ c_2=0.153 $.
This assignment is due Tuesday, November 27, 2012 at 11:59 PM. Please see the course policies regarding assignment submission, late assignments, and collaboration.
Please submit:
The Dropbox link to submit your assignment is here.
Bibliography
J. Gleick. Chaos. Viking Penguin, New York, 1987.
G. L. Baker and J. P. Gollub. Chaotic Dynamics - An Introduction. Cambridge University Press, Cambridge, England, 1990.
G. Rowland. Non-linear Phenomena in Science and Engineering. Ellis Horwood, Chichester, England, 1990.
R. Kapral and K. Showalter. Chemical Waves and Patterns. Kluwer Academic Press, Dordrecht, the Netherlands, 1995.
B. Peng, S. K. Scott, and K. Showalter. Period doubling and chaos in a three-variable autocatalator. Journal of Physical Chemistry 94:5243-5246, 1990.
F. Oz, (director). What About Bob? (film), starring Bill Murray and Richard Dreyfuss, 1991.
E. N. Lorenz. Deterministic nonperiodic flow. Journal of the Atmospheric Sciences, 20(1):130-141, March 1963.