COS 323 - Computing for the Physical and Social Sciences

Fall 2010

Assignment 2: The Pratt Truss Bridge

Due Thursday, Oct. 14

Calhoun Street Bridge, Trenton NJ

In this assignment, you will analyze the design of a truss bridge. The inputs will be the length and height of the bridge, the number of truss sections, and the amount of weight it needs to support. You will write a Matlab function that computes a matrix relating the net force on each joint to the tensile and compressive forces in the beams, and solve the resulting linear system to tell you how much tension or compression each beam undergoes. Finally, you will analyze how the optimal design depends on the number of sections and the height. Your computed forces will look like this:

1. The Pratt truss structure

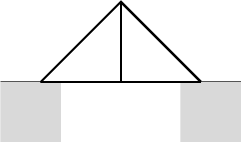
We will be working with a design called the Pratt truss, originally designed by Thomas and Caleb Pratt in 1844. Here is how it looks:

This particular (6-section) structure has 21 truss members and 12 joints. In general, we can extend the design to more or fewer sections (to keep things simple, let's only consider symmetric structures with an even number), and end up with 2n joints and 4n-3 members. Here are the designs for n = 4 and n = 2. The latter is called the King truss, and has been used since the middle ages.

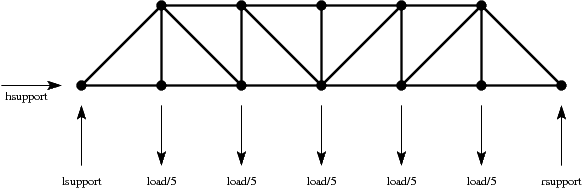
We are interested in computing the compression or tension on each beam, once forces are applied to the structure. To simplify things, we ignore the weight of the structure itself, and consider that the entire load is split evenly among the center sections while support forces are applied at the ends:

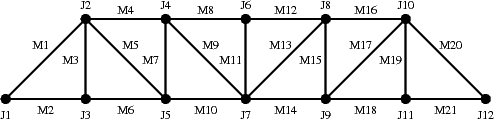
As a result of these applied forces, the truss members will have compressive and tensile forces applied to them. We adopt the convention that compression is positive and tension is negative, so a beam with a positive internal force will be pushing on the two joints it connects, while a member with negative force will be pulling. Now, we have the condition that the sum of forces at each joint must be zero. (Otherwise the joint would be accelerating - very much not what we want!) So, let's number the joints and members as follows

and consider the force diagram for J5:

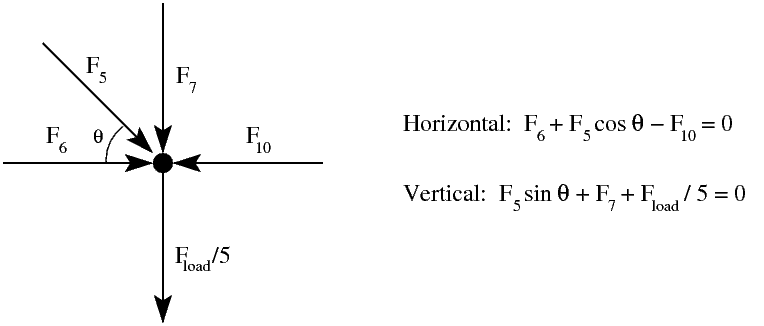
Therefore, we have two equations for each joint, one giving the horizontal balance of forces and one for vertical. The unknowns are the internal forces in each beam, plus the three support forces, giving us a total of 4n equations and 4n unknowns (the horizontal support will always be 0 in the case of a level structure, but we include it anyway to make the number of unknowns equal to the number of equations).

We ask that you adopt the convention of numbering joints and members shown above, and that you put the first joint at the origin. We provide the following three files. The first of these constructs a structure representing the bridge (span, height, and number of sections); the second is a visualization of the bridge (and later the forces on it), and the last is a helper function to draw arrows. We define span as the total length of the base of the bridge (i.e., distance from J1 to J12 above).

getBridgeStruct.m
drawBridge.m (trying to do copy figure with the figure this creates seems to crash Matlab, so be a little careful)
arrow3.m

We first need to locate the joints and members and figure out which joints are attached to which members. You can do so by completing the files:

getJointPos.m - takes in a bridge and a joint index, and returns the (x, y) position of the joint. Note that the range in x and y of the positions should pay attention to the span and height passed in the bridgeStruct.
getMemberJoints.m - takes in a bridge and a member index, and returns the indices of the two joints the member is attached to

drawBridge makes calls to the above two functions; once those are completed, you can use it to check the member and joint positions.

2. Solving the equations

Write a Matlab function that takes as input:

A bridge struct.
The total load to be applied to the bridge - spread this out evenly among the lower joints other than the two at the ends.

The function should return a matrix A and vector b such that

The dimension of A is 4n by 4n, and the dimension of b is 4n by 1.
The equation Ax=b encodes the joint constraints, assuming the elements of x are the unknowns (internal forces and support forces).

The rows of A represent equations for each joint, and the columns represent the dependence on an unknown force. Any arrangement of the rows and columns of A (and b), and a multiplication of each equation by a non-zero scalar will produce an equivalent system. To make your arrangement compatible with the visualization we provide, we ask that you follow these conventions:

The joints are aranged in order, with the x (horizontal) equation followed by the y (vertical) equation. So the first row has the x equation for joint 1, the next row has y equation for joint 1, then x equation for joint 2, and so on.
The forces (columns) are arranged as follows. First are the internal forces of the members, in order (columns 1 to 4n-3). Next is the lsupport, rsupport, and hsupport. (Can you figure out analytically what the last three forces ought to be?)
The coefficients in A represent the forces as they are, unscaled, and the values in b are negative of the forces (since we need to choose one side of the equation to negate).

The thing that makes this tricky is dealing with n as a parameter to the function. You may find it easiest to first create A as a matrix full of zeros

A = zeros(4*n,4*n);

then loop through the members, or through the joints, filling in the appropriate nonzero entries. Think carefully about how you want to do this and how you might be able to use functions from the previous part. You did a lot of case analysis in the previous part that you do not want to repeat.

Once you can create A and b, solving for x is as easy as

x = A\b;

With drawBridge, you can visualize the bridge, the bridge with load forces (from b), and the bridge with internal forces (using b and x). Compression forces are blue, and tension forces are red. Make sure you are happy with the solutions; if you wish, you can test a particular case here:

http://www.jhu.edu/~virtlab/bridge/bridge.htm

Produce visualizations of forces for two bridges: with 4 sections, of span 4, of heights 1 and 2, and save these as images.

3. Analysis

Look at the pattern of compressive and tensile forces in the structure. Are the innermost diagonal members under compression or tension? Which beams have the greatest stresses for very tall bridges? For very short bridges?

Explain why the Calhoun Street Bridge in Trenton NJ shown above can use cables for the diagonal members.

Compute the maximum compressive or tensile force in any beam in the bridge (using the max and abs functions). Assuming all the beams are made with the same cross section, this will determine how thick the beams have to be. Since the capacity of a beam is proportional to its cross sectional area, and since the cost of the materials is proportional to length times area, the materials cost of the bridge is just proportional to

|max force| * (total length of beams)

(ignoring things like safety margins, cost of the joints, resistance to wind forces, etc.) So, you can evaluate different designs for bridges that use different values for height and n (while holding total load and span constant):

This graph shows the cost (y axis) for a given height-to-span ratio (x axis), for n = 2 (red) and n = 6 (blue). Try to produce graphs such as this for values of n from 2 to 10. Based on these, what can you say about when it's best to use different values of n? (e.g., for fairly low bridges, is it better to use more or fewer sections?)

4. Optimization

Implement the golden-section search method for function minimzation. Use it to find the optimal height-to-width ratio for any given n. Generate and submit a plot showing the optimal height-to-width ratio as a function of n.

Submitting

This assignment is due Thursday, October 14, 2010 at 11:59 PM. Please see the general notes on submitting your assignments, as well as the late policy and the collaboration policy.

Please submit:

Your code from sections 1-4.
Your pictures of the requested two bridges in section 2.
Graph or graphs for n = 2 through 10 in section 3.
Graph for optimal height-to-width ratio in section 4.
Answers to the questions in the README.txt
(Note that this includes a few general questions as well as questions related to the assignment.)

The Dropbox link to submit your assignment is here.

If you're feeling ambitious, you can also investigate some of the other designs illustrated here, such as the Warren and Howe trusses.

Disclaimer: I am not a structural engineer. I don't even play one on TV. Consult someone experienced before designing any real bridges. --- smr

Last update 3-Oct-2010 19:04:14

smr at princeton edu